Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Differential Equations

Short Answer Type

311.

If space straight y space equals space Pe to the power of ax plus Qe to the power of bx

show that

straight d to the power of 2 straight y end exponent over dx squared minus left parenthesis straight a plus straight b right parenthesis dy over dx plus aby space equals 0

111 Views

312.

If space straight x equals cost left parenthesis 3 minus 2 cos squared straight t right parenthesis space and space straight y equals sint left parenthesis 3 minus 2 sin squared straight t right parenthesis comma space find space the space value space of space dy over dx at space straight t equals straight pi over 4.

107 Views

313.

Find the particular solution of the differential equation $log open parentheses dy over dx close parentheses equals 3 straight x plus 4 straight y comma space given space that space straight y space equals space 0 comma space when space straight x equals space 0.$

120 Views

314.

Write the degree of the differential equation $straight x cubed open parentheses fraction numerator straight d squared straight y over denominator dx squared end fraction close parentheses squared space plus space open parentheses dy over dx close parentheses to the power of 4 space equals space 0$

180 Views

315.

The amount of pollution content added in air in city due to x-diesel vehicles is given by 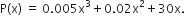$straight P left parenthesis straight x right parenthesis space equals space 0.005 straight x cubed plus 0.02 straight x squared plus 30 straight x.$ Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions.

225 Views

316.

Show that the function f in $straight A space equals space straight R to the power of minus open curly brackets 2 over 3 close curly brackets space defined space as space straight f left parenthesis straight x right parenthesis space equals space fraction numerator 4 straight x plus 3 over denominator 6 straight x minus 4 end fraction space is space one minus one space and space onto. space Hence space find space straight f to the power of negative 1 end exponent.$

130 Views

317.
Differentiate the following function with respect to x: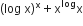
$left parenthesis log space straight x right parenthesis to the power of straight x plus straight x to the power of log straight x$

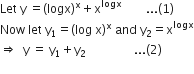
$Let space straight y space equals left parenthesis logx right parenthesis to the power of straight x plus straight x to the power of logx space space space space space space space space... left parenthesis 1 right parenthesis Now space let space straight y subscript 1 equals left parenthesis log space straight x right parenthesis to the power of straight x space and space straight y subscript 2 equals straight x to the power of logx rightwards double arrow space space straight y space equals space straight y subscript 1 plus straight y subscript 2 space space space space space space space space space space space space space space space space... left parenthesis 2 right parenthesis$
Differentiating (2), w.r.t.x,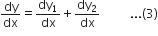
$dy over dx equals dy subscript 1 over dx plus dy subscript 2 over dx space space space space space space space space space space... left parenthesis 3 right parenthesis$

Now consider

straight y subscript 1 space equals space left parenthesis log space straight x right parenthesis to the power of straight x

Taking log on both sides,

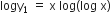
logy subscript 1 space equals space straight x space log left parenthesis log space straight x right parenthesis

Differentiating, w.r.t.x, we get

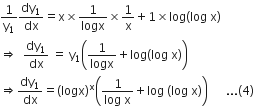
1 over straight y subscript 1 dy subscript 1 over dx equals straight x cross times 1 over logx cross times 1 over straight x plus 1 cross times log left parenthesis log space straight x right parenthesis rightwards double arrow space space dy subscript 1 over dx space equals space straight y subscript 1 open parentheses 1 over logx plus log left parenthesis log space straight x right parenthesis close parentheses rightwards double arrow dy subscript 1 over dx equals left parenthesis logx right parenthesis to the power of straight x open parentheses fraction numerator 1 over denominator log space straight x end fraction plus log space left parenthesis log space straight x right parenthesis close parentheses space space space space space space... left parenthesis 4 right parenthesis

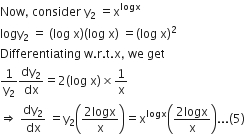
Now comma space consider space straight y subscript 2 space equals straight x to the power of logx logy subscript 2 space equals space left parenthesis log space straight x right parenthesis left parenthesis log space straight x right parenthesis space equals left parenthesis log space straight x right parenthesis squared Differentiating space straight w. straight r. straight t. straight x comma space we space get 1 over straight y subscript 2 dy subscript 2 over dx equals 2 left parenthesis log space straight x right parenthesis cross times 1 over straight x rightwards double arrow space dy subscript 2 over dx space equals straight y subscript 2 open parentheses fraction numerator 2 logx over denominator straight x end fraction close parentheses equals straight x to the power of logx open parentheses fraction numerator 2 logx over denominator straight x end fraction close parentheses... left parenthesis 5 right parenthesis

Using equations (3), (4) and (5), we get:

dy over dx equals left parenthesis log space straight x right parenthesis to the power of straight x open square brackets 1 over logx plus log left parenthesis log space straight x right parenthesis close square brackets plus straight x to the power of logx open parentheses fraction numerator 2 logx over denominator straight x end fraction close parentheses

142 Views

318.

If space straight y space equals space log space open square brackets straight x space plus space square root of straight x squared plus space straight a squared end root close square brackets comma space show space that space left parenthesis straight x squared space plus space straight a squared right parenthesis space fraction numerator straight d squared straight y over denominator dx squared end fraction space plus straight x dy over dx space equals space 0

186 Views

319.

If $straight x equals straight a space sint space and space straight y space equals space straight a open parentheses cost plus log space tan straight t over 2 close parentheses space find space fraction numerator straight d squared straight y over denominator dx squared end fraction$

500 Views

Long Answer Type

320.

Show that the differential equation 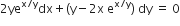$2 ye to the power of straight x divided by straight y end exponent dx plus left parenthesis straight y minus 2 straight x space straight e to the power of straight x divided by straight y end exponent right parenthesis space dy space equals space 0$ is homogeneous. Find the particular solution of this differential equation, given that x = 0 when y = 1.