 Short Answer Type
Short Answer TypeThe amount of pollution content added in air in city due to x-diesel vehicles is given by 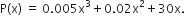 Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions.
Find the marginal increase in pollution content when 3 diesel vehicles are added and write which value is indicated in the above questions.
 Long Answer Type
Long Answer TypeShow that the differential equation 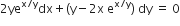 is homogeneous. Find the particular solution of this differential equation, given that x = 0 when y = 1.
is homogeneous. Find the particular solution of this differential equation, given that x = 0 when y = 1.
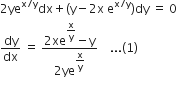
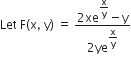
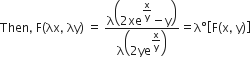
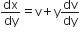
 in equation (1), we get
in equation (1), we get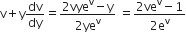
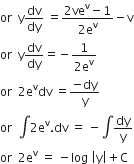
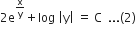

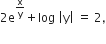 which is the particular solution of the given differential equation.
which is the particular solution of the given differential equation. 