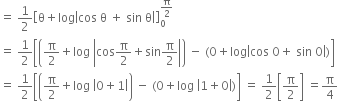Long Answer Type
Long Answer Type Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Short Answer Type
Short Answer TypeShow that:![]()
Let I =В ![]()
Put x = a sin Оё, В В В вҲҙ dx = a cos Оё dОё
When x = 0, a sin Оё = 0 вҮ’ sin Оё = 0 вҮ’ Оё = 0
when x = a,В ![]()
![]()
В В В В В ![]()
В В В В В ![]()
В В В В В
В В В В В В