 Short Answer Type
Short Answer Type Long Answer Type
Long Answer Type Multiple Choice Questions
Multiple Choice QuestionsTwo sides of a rhombus are along the lines, x−y+1=0 and 7x−y−5=0. If its diagonals intersect at (−1, −2), then which one of the following is a vertex of this rhombus?
(−3, −9)
(−3, −8)
(1/3, -8/3)
(1/3, -8/3)
C.
(1/3, -8/3)
As the given lines x-y +1 =0 and 7x-y-5 = 0 are not parallel, therefore they represent the adjacent sides of the rhombus.
On solving x-y+1 = 0 adn 7x - y -5 = 0. we get x =1 and y =2
Thus, one of the vertex is A(1,2)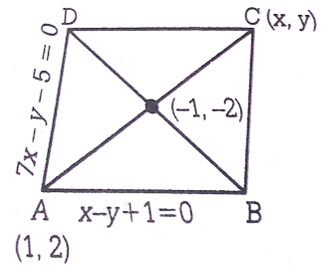
Let the coordinate of point C be (x,y)
Then, 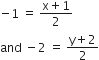
⇒ x+1 =- 2 and y =-4-2
⇒ x=-3 and y =-6
Hence, coordinates of C = (-3,-6)
Note that, vertices B and D will satisfy x-y +1 =0 and 7x - y-5 = 0, therefore the coordinate of vertex D is (1/3, -8/3)
The centres of those circles which touch the circle, x2+y2−8x−8y−4=0, externally and also touch the x-axis, lie on:
a circle
an ellipse which is not a circle
a hyperbola.
a hyperbola.
