 Multiple Choice Questions
Multiple Choice QuestionsThe equation of the tangent to the curve y = x +4/x2, that is parallel to the x-axis, is
y= 0
y= 1
y= 2
y= 2
D.
y= 2
We have, 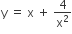
On differentiating w.r.t x, we get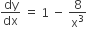
since the tangent is parallel to X- axis, therefore
dy/dx = 0
⇒ x3 = 8
⇒ x = 2 abd y =3
Let cos (α + β) = 4/5 and let sin (α - β) = 5/13, where 0 ≤α,β ≤ π/4. Then tan 2α is equal to
25/16
56/33
19/12
19/12
The differential equation which represents the family of curves y=c1ec2xe, where c1 and c2 are arbitrary constants, is
y' =y2
y″ = y′ y
yy″ = y′
yy″ = y′
The solution of the differential equation 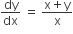 satisfying the condition y (1) = 1 is
satisfying the condition y (1) = 1 is
y = ln x + x
y = x ln x + x2
y = xe(x−1)
y = xe(x−1)
For each t ∈R, let [t] be the greatest integer less than or equal to t. Then
does not exist (in R)
is equal to 0
is equal to 15
is equal to 120
Let f(x) = x13 + x11 + x9 + x7 + x5 + x3 + x + 19. Then , f(x) = 0 has
13 real roots
only one positive and only two negative real roots
not more than one real root
has two positive and one negative real root
