• -1/4

• 1/2

• 1

• 1

The equation of the tangent to the curve y = x +4/x², that is parallel to the x-axis, is

• y= 0

• y= 1

• y= 2 

• y= 2 

Let cos (α + β) = 4/5 and let sin (α - β) = 5/13, where 0 ≤α,β ≤ π/4. Then tan 2α is equal to

• 25/16

• 56/33

• 19/12

• 19/12

• 1/4

• 1/24

• 1/16

• 1/16

If 5(tan²x – cos²x) = 2cos ²x + 9, then the value of cos⁴x is

• -7/9

• -3/5

• 1/3

• 1/3

The differential equation which represents the family of curves y=c₁e^c₂xe, where c₁ and c₂ are arbitrary constants, is

• y' =y²

•  y″ = y′ y

• yy″ = y′

• yy″ = y′

The solution of the differential equation 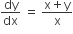   satisfying the condition y (1) = 1 is  

• y = ln x + x

• y = x ln x + x²

•  y = xe^(x−1)

•  y = xe^(x−1)

If  then the values of a and b, are

For each t ∈R, let [t] be the greatest integer less than or equal to t. Then

$\underset{x\to 0^{+}}{lim} x\left(\left[\frac{1}{x}\right]+\left[\frac{2}{x}\right]+......+\left[\frac{15}{x}\right]\right)$

• does not exist (in R)

• is equal to 0

• is equal to 15

• is equal to 120

110.

Let f(x) = x¹³ + x¹¹ + x⁹ + x⁷ + x⁵ + x³ + x + 19. Then , f(x) = 0 has

• 13 real roots

• only one positive and only two negative real roots

• not more than one real root

• has two positive and one negative real root