Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Long Answer Type

261. Find the coordinates of the foot of perpendicular from the point (2, 2, 7) to the plane 3 x – y – z = 7. Also find the length of perpendicular.

86 Views

262. Find the image of the point (1, 2, 3) in the plane x + 2y + 4z = 38.

111 Views

263. Find the Cartesian as well as the vector equation of the planes passing through the intersection of the planes $straight r with rightwards arrow on top space. left parenthesis 2 space straight i with hat on top space plus space 6 space straight j with hat on top right parenthesis space plus space 12 space equals space 0 space space and space straight r with rightwards arrow on top. space space open parentheses 3 space straight i with hat on top space minus space straight j with hat on top space plus space 4 space straight k with hat on top close parentheses space equals space 0 comma$ which are at unit distance from the origin.

The equation of first plane is

straight r with rightwards arrow on top space. space open parentheses 2 straight i with hat on top space plus space 6 straight j with hat on top close parentheses space plus space 12 space equals space 0

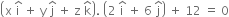
open parentheses straight x space straight i with hat on top space plus space straight y space straight j with hat on top space plus space straight z space straight k with hat on top close parentheses. space open parentheses 2 space straight i with hat on top space plus space 6 space straight j with hat on top close parentheses space plus space 12 space equals space 0

or space space space 2 straight x plus 6 straight y plus 12 space equals space 0 comma space space space space space space or space space space straight x plus 3 straight y plus 6 space equals space 0 space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis

The equation of second plane is

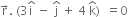
straight r with rightwards arrow on top. space left parenthesis 3 straight i with hat on top space minus space straight j with hat on top space plus space 4 space straight k with hat on top right parenthesis space space equals 0

open parentheses straight x space straight i with hat on top space plus space straight y space straight j with hat on top space plus space straight z space straight k with hat on top close parentheses space. space open parentheses 3 space straight i with hat on top space minus space straight j with hat on top space plus space space 4 space straight k with hat on top close parentheses space equals space 0

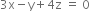3 straight x minus straight y plus 4 straight z space equals space 0

...(2)
The equation of any plane through the intersection of planes (1) and (2) is
(x + 3 y + 6) + k (3 x – y + 4 z) = 0
or (3 k + l).x + (–k + 3)y + 4 kz + 6 = 0 ...(3)
From given condition,
perpendicular distance of origin (0, 0, 0) from plane (3) = 1

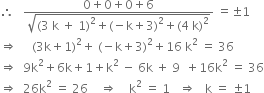therefore space space space fraction numerator 0 plus 0 plus 0 plus 6 over denominator square root of left parenthesis 3 space straight k space plus space 1 right parenthesis squared plus left parenthesis negative straight k plus 3 right parenthesis squared plus left parenthesis 4 space straight k right parenthesis squared end root end fraction space equals plus-or-minus 1 rightwards double arrow space space space space space left parenthesis 3 straight k plus 1 right parenthesis squared plus space left parenthesis negative straight k plus 3 right parenthesis squared plus 16 space straight k squared space equals space 36 rightwards double arrow space space 9 straight k squared plus 6 straight k plus 1 plus straight k squared space minus space 6 straight k space plus space 9 space space plus 16 straight k squared space equals space 36 rightwards double arrow space space 26 straight k squared space equals space 26 space space space space rightwards double arrow space space space space straight k squared space equals space 1 space space space rightwards double arrow space space space straight k space equals space plus-or-minus 1

Taking k = 1, from (3), we get,

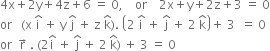4 straight x plus 2 straight y plus 4 straight z plus 6 space equals space 0 comma space space space space or space space space space 2 straight x plus straight y plus 2 straight z plus 3 space equals space 0 or space space space left parenthesis straight x space straight i with hat on top space plus space straight y space straight j with hat on top space plus space straight z space straight k with hat on top right parenthesis. space open parentheses 2 space straight i with hat on top space plus space straight j with hat on top space plus space 2 space straight k with hat on top close parentheses plus space 3 space space equals space 0 or space space straight r with rightwards arrow on top space. space left parenthesis 2 straight i with hat on top space plus space straight j with hat on top space plus space 2 space straight k with hat on top right parenthesis space plus space 3 space equals space 0

Taking k = – 1, from (3), we get,

negative 2 straight x plus 4 space straight y minus 4 straight z plus 6 space equals space 0 comma space space space space or space space space straight x minus 2 straight y plus 2 straight z minus 3 space equals space 0

or space space space left parenthesis straight x space straight i with hat on top space plus space straight y space straight j with hat on top space plus space straight z space straight k with hat on top right parenthesis. space space open parentheses straight i with hat on top space minus space 2 space straight j with hat on top space plus space 2 space straight k with hat on top close parentheses space minus space 3 space equals 0

or space space space space straight r with rightwards arrow on top. space open parentheses straight i with hat on top space minus space space 2 space straight j with hat on top space plus space 2 space straight k with hat on top close parentheses minus 3 space equals space 0

The required cartesian equations are
2x + y + 2z + 3 = 0, x – 2y + 2z — 3 = 0
and vector equations are

straight r with rightwards arrow on top. space left parenthesis 2 space straight i with hat on top space plus space straight j with hat on top space plus space 2 space straight k with hat on top right parenthesis space plus space 3 space equals space 0 space space space and space space straight r with rightwards arrow on top. space space open parentheses straight i with hat on top space minus space 2 space straight j with hat on top space plus space 2 space straight k with hat on top close parentheses space minus space 3 equals 0.

77 Views

Short Answer Type

264. Prove that if a plane has the intercepts a, b, c and is at a distance p units from the origin, then

1 over straight a squared plus 1 over straight b squared plus 1 over straight c squared space equals space 1 over straight p squared.

105 Views

Long Answer Type

265. A variable plane which remains at a constant distance 3p from the origin, cuts the co-ordinate axes at A, B, C. Show that the locus of the centroid of the triangle ABC is

1 over straight x squared plus 1 over straight y squared plus 1 over straight z squared space equals 1 over straight p squared.

391 Views

266. A variable plane is at a constant distance p from the origin and meets the axes in A, B and C respectively, then show that locus of the centroid of the triangle ABC is

1 over straight x squared plus 1 over straight y squared plus 1 over straight z squared space equals space 9 over straight p squared.

105 Views

Short Answer Type

267. If a variable plane at a constant distance p from the origin meets the coordinate axes in points A, B and C respectively. Through these points, planes are drawn parallel to the coordinate planes. Then show that the locus of the point of intersection is