Previous Year Papers

Download Solved Question Papers Free for Offline Practice and view Solutions Online.

Test Series

Take Zigya Full and Sectional Test Series. Time it out for real assessment and get your results instantly.

Test Yourself

Practice and master your preparation for a specific topic or chapter. Check you scores at the end of the test.

Three Dimensional Geometry

Long Answer Type

261. Find the coordinates of the foot of perpendicular from the point (2, 2, 7) to the plane 3 x – y – z = 7. Also find the length of perpendicular.

86 Views

262. Find the image of the point (1, 2, 3) in the plane x + 2y + 4z = 38.

111 Views

263. Find the Cartesian as well as the vector equation of the planes passing through the intersection of the planes

straight r with rightwards arrow on top space. left parenthesis 2 space straight i with hat on top space plus space 6 space straight j with hat on top right parenthesis space plus space 12 space equals space 0 space space and space straight r with rightwards arrow on top. space space open parentheses 3 space straight i with hat on top space minus space straight j with hat on top space plus space 4 space straight k with hat on top close parentheses space equals space 0 comma

which are at unit distance from the origin.

77 Views

Short Answer Type

264. Prove that if a plane has the intercepts a, b, c and is at a distance p units from the origin, then

1 over straight a squared plus 1 over straight b squared plus 1 over straight c squared space equals space 1 over straight p squared.

105 Views

Long Answer Type

265. A variable plane which remains at a constant distance 3p from the origin, cuts the co-ordinate axes at A, B, C. Show that the locus of the centroid of the triangle ABC is $1 over straight x squared plus 1 over straight y squared plus 1 over straight z squared space equals 1 over straight p squared.$

Let O be the origin and OA = a, OB = b, OC = c
∴ equation of plane passing through A, B and C is
$straight x over straight a plus straight y over straight b plus straight z over straight c equals 1$

or $straight x over straight a plus straight y over straight b plus straight z over straight c minus 1 space equals space 0$
From the given condition, 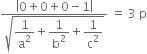$fraction numerator open vertical bar 0 plus 0 plus 0 minus 1 close vertical bar over denominator square root of begin display style 1 over straight a squared end style plus begin display style 1 over straight b squared end style plus begin display style 1 over straight c squared end style end root end fraction space equals space 3 space straight p$
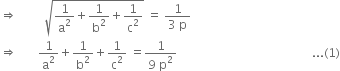
$rightwards double arrow space space space space space space space space space square root of 1 over straight a squared plus 1 over straight b squared plus 1 over straight c squared end root space equals space fraction numerator 1 over denominator 3 space straight p end fraction rightwards double arrow space space space space space space space 1 over straight a squared plus 1 over straight b squared plus 1 over straight c squared space equals fraction numerator 1 over denominator 9 space straight p squared end fraction space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space space... left parenthesis 1 right parenthesis$

Now A, B, C are (a, 0, 0), (0, b, 0), (0, c, 0) respectively.
Let (x₁ , y₁ , z₁ ) be the centroid of ΔABC.
$therefore space space space straight x subscript 1 space equals space fraction numerator straight a plus 0 plus 0 over denominator 3 end fraction comma space space space straight y subscript 1 space equals space fraction numerator 0 plus straight b plus 0 over denominator 3 end fraction comma space straight z subscript 1 space equals space fraction numerator 0 plus 0 plus 0 over denominator 3 end fraction therefore space space space space straight a space equals space 3 space straight x subscript 1 comma space space space space straight b space equals space 3 space straight y subscript 1 comma space space space straight c space equals space 3 space straight z subscript 1$

Putting values of a, b,c in (1), we get

fraction numerator 1 over denominator 9 space straight x subscript 1 squared end fraction plus fraction numerator 1 over denominator 9 space straight y subscript 1 squared end fraction plus fraction numerator 1 over denominator 9 space straight z subscript 1 squared end fraction space equals space fraction numerator 1 over denominator 9 space straight p squared end fraction

1 over straight x subscript 1 squared plus 1 over straight y subscript 1 squared plus 1 over straight z subscript 1 squared space equals space 1 over straight p squared

therefore

locus of centroid

open parentheses straight x subscript 1 comma space straight y subscript 1 comma space straight z subscript 1 close parentheses

1 over straight x squared plus 1 over straight y squared plus 1 over straight z squared space equals space 1 over straight p squared.

391 Views

266. A variable plane is at a constant distance p from the origin and meets the axes in A, B and C respectively, then show that locus of the centroid of the triangle ABC is

1 over straight x squared plus 1 over straight y squared plus 1 over straight z squared space equals space 9 over straight p squared.

105 Views

Short Answer Type

267. If a variable plane at a constant distance p from the origin meets the coordinate axes in points A, B and C respectively. Through these points, planes are drawn parallel to the coordinate planes. Then show that the locus of the point of intersection is