Let α, β be such that π < α - β < 3π. If sinα + sinβ = -21/65 and cosα + cosβ = -27/65, then the value of cos α-β/2 is

• 
• 

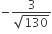
• 6/65

• 6/65

632.

If 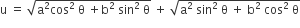 then the difference between the maximum and minimum values of 2 u is given by

• 2(a² + b²)

• 2(a²-b²)

• (a+b)²

• (a+b)²

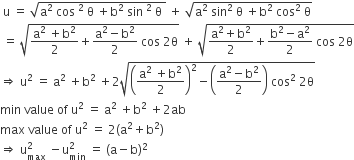
The sides of a triangle are sinα, cosα and  for some 0 < α < π/2 . Then the greatest angle of the triangle is

• 60^o

• 120^o

• 360^o

• 360^o

A person standing on the bank of a river observes that the angle of elevation of the top of a tree on the opposite bank of the river is 60^o and when he retires 40 meters away from the tree the angle of elevation becomes 30^o. The breadth of the river is

• 20 m

• 30 m

• 40 m

• 40 m

The equation sin x(sin(x) + cos(x)) = k has real solutions, where k is a real number. Then,

• $0 \le \mathrm{k} \le \frac{1 + \sqrt{2}}{2}$

• $2 - \sqrt{3} \le \mathrm{k} \le 2 + \sqrt{3}$

• $0 \le \mathrm{k} \le 2 - \sqrt{3}$

• $\frac{1 - \sqrt{2}}{2} \le \mathrm{k} \le \frac{1 + \sqrt{2}}{2}$

The cosine of the angle between any two diagonals of a cube is

• $\frac{1}{3}$

• $\frac{1}{2}$

• $\frac{2}{3}$

• $\frac{1}{\sqrt{3}}$

The value of $\cos \left(15°\right)\cos \left(7\frac{1°}{2}\right)\sin \left(7\frac{1°}{2}\right)$ is

• $\frac{1}{2}$

• $\frac{1}{8}$

• $\frac{1}{4}$

• $\frac{1}{16}$

If z = $\sin \left(\mathrm{\theta }\right) - \mathrm{icos}\left(\mathrm{\theta }\right)$, then for any integer n,

• ${\mathrm{z}}^{\mathrm{n} }+\hspace{0.17em}\frac{1}{{\mathrm{z}}^{\mathrm{n}}} = 2\cos \left(\frac{\mathrm{n\pi }}{2} - \mathrm{n\theta }\right)$

• ${\mathrm{z}}^{\mathrm{n} }+\hspace{0.17em}\frac{1}{{\mathrm{z}}^{\mathrm{n}}} = 2\sin \left(\frac{\mathrm{n\pi }}{2} - \mathrm{n\theta }\right)$

• ${\mathrm{z}}^{\mathrm{n} }-\hspace{0.17em}\frac{1}{{\mathrm{z}}^{\mathrm{n}}} = 2\mathrm{isin}\left( \mathrm{n\theta } - \frac{\mathrm{n\pi }}{2}\right)$

• ${\mathrm{z}}^{\mathrm{n} }-\hspace{0.17em}\frac{1}{{\mathrm{z}}^{\mathrm{n}}} = 2\mathrm{icos}\left(\frac{\mathrm{n\pi }}{2} - \mathrm{n\theta }\right)$

The minimum value of $\cos \left(\mathrm{\theta }\right) + \sin \left(\mathrm{\theta }\right) + \frac{2}{\sin \left(\mathrm{\theta }\right)} \mathrm{for} \mathrm{\theta } \in \left(0, \raisebox{1ex}{$\mathrm{\pi }$}\!\left/ \!\raisebox{-1ex}{$2$}\right.\right)$

• $2 + \sqrt{2}$

• 2

• 1 + $\sqrt{2}$

• $2\sqrt{2}$

If $\cot \left(\frac{2\mathrm{x}}{3}\right) + \tan \left(\frac{\mathrm{x}}{3}\right) = \csc \left(\frac{\mathrm{kx}}{3}\right)$, then the value of k is

• 1

• 2

• 3

• - 1