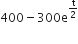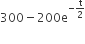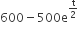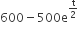Multiple Choice Questions
Multiple Choice QuestionsIf one of the diameters of the circle, given by the equation, x2+y2−4x+6y−12=0, is a chord of a circle S, whose centre is at (−3, 2), then the radius of S is:
5√2
5√3
5
10
Let P be the point on the parabola, y2=8x which is at a minimum distance from the centre C of the circle, x2+(y+6)2=1. Then the equation of the circle, passing through C and having its centre at P is:
x2+y2−4x+8y+12=0
x2+y2−x+4y−12=0
x2+y2− 4 x +2y−24=0
x2+y2− 4 x +2y−24=0
The eccentricity of the hyperbola whose length of the latus rectum is equal to 8 and the length of its conjugate axis is equal to half of the distance between its foci, is:
4/3
4/√3
2/√3
√3
The area (in sq units) of the region described by {x,y): y2 ≤ 2x and y ≥ 4x-1} is
7/32
5/64
15/64
15/64
The area (in sq units) of the quadrilateral formed by the tangents at the end points of the latera recta to the ellipse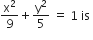
27/4
18
27/2
27/2
Let O be the vertex and Q be nay point on the parabola x2 = 8y. If the point P divides the line segment OQ internally in the ratio 1:3 then the locus of P is
x2= y
y2 =x
y2 =2x
y2 =2x
If =-1 and x =2 are extreme points of f(x) =α log|x| + βx2 +x, then
α = -6, β = 1/2
α = -6, β = -1/2
α = 2, β = -1/2
α = 2, β = -1/2
Let the population of rabbits surviving at a time t be governed by the differential equation.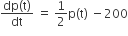 If p(0) = 100 then p(t) is equal to
If p(0) = 100 then p(t) is equal to