 Multiple Choice Questions
Multiple Choice QuestionsA body weighing 13 kg is suspended by two strings 5 m and 12 m long, their other ends being fastened to the extremities of a rod 13 m long. If the rod be so held that the body hangs immediately below the middle point. The tensions in the strings are
12 kg and 13 kg
5 kg and 5 kg
5 kg and 12 kg
5 kg and 12 kg
If the difference between the roots of the equation x2 + ax + 1 = 0 is less than 5 , then the set of possible values of a is
(−3, 3)
(−3, ∞)
(3, ∞)
(3, ∞)
If the roots of the quadratic equation x2 + px + q = 0 are tan30° and tan15°, respectively then the value of 2 + q − p is
2
3
0
0
All the values of m for which both roots of the equations x2 − 2mx + m2 − 1 = 0 are greater than −2 but less than 4, lie in the interval
−2 < m < 0
m > 3
−1 < m < 3
−1 < m < 3
If the cube roots of unity are 1, ω, ω2 then the roots of the equation (x – 1)3 + 8 = 0, are
-1 , - 1 + 2ω, - 1 - 2ω2
-1 , -1, - 1
-1 , 1 - 2ω, 1 - 2ω2
-1 , 1 - 2ω, 1 - 2ω2
The value of α for which the sum of the squares of the roots of the equation x2 – (a – 2)x – a – 1 = 0 assume the least value is
1
0
3
3
If roots of the equation x2 – bx + c = 0 be two consectutive integers, then b2 – 4c equals
– 2
3
2
2
If the coefficient of x7 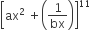 in equals the coefficient of x-7 in
in equals the coefficient of x-7 in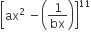 then a and b satisfy the relation
then a and b satisfy the relation
a – b = 1
a + b = 1
a/b =1
a/b =1
If z1 and z2 are two non-zero complex numbers such that |z1 + z2| = |z1| + |z2| then argz1 – argz2 is equal to
π/2
-π
0
0
