 Multiple Choice Questions
Multiple Choice QuestionsIf (10)9 +2 (11)2(10)7 + .....+10 (11)9 = K(10)9, then k is equal to
121/10
441/100
100
100
A multiple choice examination has 5 questions. Each question has three alternative answers of which exactly one is correct. The probability that a student will get 4 or more correct answers just by guessing is
17/35
13/35
11/35
11/35
If n is a positive integer, then 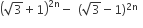 is
is
an irrational number
an odd positive integer
an even positive integer
an even positive integer
The value of
(21C1 – 10C1) + (21C2 – 10C2) + (21C3 – 10C3) + (21C4 – 10C4) + .... +
(21C10 – 10C10) is
220 – 210
221 – 211
221 – 210
221 – 210
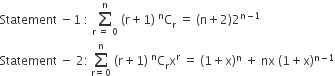
Statement −1 is false, Statement −2 is true
Statement −1 is true, Statement −2 is true, Statement −2 is a correct explanation for Statement −1
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
In the binomial expansion of (a - b)n, n ≥ 5, the sum of 5th and 6th terms is zero, then
a/b equals
5/n −4
6 /n −5
n -5 /6
n -5 /6
