 Multiple Choice Questions
Multiple Choice QuestionsThe locus of the foot of perpendicular drawn from the centre of the ellipse x2+3y2 =6 on any tangent to it is
(x2-y2)2 = 6x2+2y2
(x2-y2)2 = 6x2 -2y2
(x2+y2)2 = 6x2+2y2
(x2+y2)2 = 6x2+2y2
The slope of the line touching both the parabolas y2 = 4x and x2-32y is
1/2
3/2
1/8
1/8
A.
1/2
For parabola, y2 = 4x
Let y = mx + 1/m be tangent line and it touches the parabola x2=-32y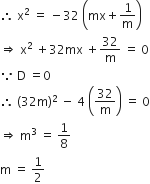
The circle passing through (1,-2) and touching the axis of x at (3,0) also passes through the point
(-5,2)
(2,-5)
(5,-2)
(5,-2)
The equation of the circle passing through the foci of the ellipse 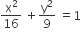 and having centre at (0,3) is
and having centre at (0,3) is
x2+y2-6y-7 =0
x2+y2-6y+7 =0
x2+y2-6y-5 =0
x2+y2-6y-5 =0
Let Tn be the number of all possible triangles formed by joining vertices of an n-sided regular polygon. If Tn+1 − Tn = 10, then the value of n is
7
5
10
10
Given A circle, 2x2 + 2y2= 5 and parabola, 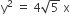
Statement I An equation of a common tangent to these curves is 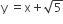
Statement II If the line 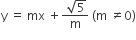 is the common tangent, then m satisfies m4-3m2+2 =0
is the common tangent, then m satisfies m4-3m2+2 =0
Statement I is true, Statement II is true; Statement II is a correct explanation for statement I
Statement I is true, Statement II is true; Statement II is not a correct explanation for statement I
Statement I is true, Statement II is false
Statement I is true, Statement II is false
Statement I An equation of a common tangent to the parabola 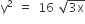 and the ellipse 2x2 +y2 =4 is
and the ellipse 2x2 +y2 =4 is 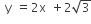 .
.
Statement II If the line 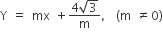 is a common tangent to the parabola
is a common tangent to the parabola 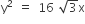 and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
The area bounded between the parabolas x2=y/4 and x2 = 9y, and the straight line y = 2 is

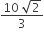
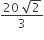
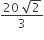
If z ≠ 1 and 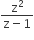 is real, then the point represented by the complex number z lies
is real, then the point represented by the complex number z lies
either on the real axis or on a circle passing through the origin
on a circle with centre at the origin
either on the real axis or on a circle not passing through the origin
either on the real axis or on a circle not passing through the origin
The length of the diameter of the circle which touches the x-axis at the point (1, 0) and passes through the point (2, 3) is
10/3
3/5
6/5
6/5
