 Multiple Choice Questions
Multiple Choice QuestionsA satellite is revolving in a circular orbit at a height ‘h’ from the earth’s surface (radius of earth R ; h<<R). The minimum increase in its orbital velocity required, so that the satellite could escape from the earth’s gravitational field, is close to: (Neglect the effect of atmosphere.)




A uniform string of length 20 m is suspended from a rigid support. A short wave pulse is introduced at its lowest end. It starts moving up the string. The time taken to reach the support is: (take g = 10 ms−2 )

2s


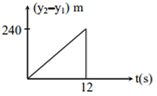
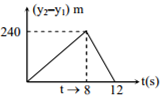
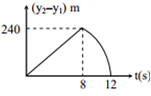
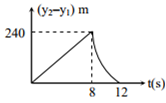
Two stones are thrown up simultaneously from the edge of a cliff 240 m high with an initial speed of 10 m/s and 40 m/s respectively. Which of the following graph best represents the time variation of relative position of the second stone with respect to the first? (Assume stones do not rebound after hitting the ground and neglect air resistance, take g = 10 m/s2 )
From a solid sphere of mass M and radius R, a spherical portion of radius R/2 is removed, as shown in the figure. Taking gravitational potential V = 0 at r = ∞, the potential at the centre of the cavity thus formed is (G = gravitational constant)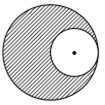
-GM/2R
-GM/R
-2GM/3R
-2GM/R
From the tower of height H, a particle is thrown vertically upwards with a speed u. The time taken by the particle to hit the ground is n times that taken by it to reach the highest point of its path. The relation between H,u and n is
2gH = n2u2
gH = (n-2)2u2
2gH = nu2(n-2)2u2
2gH = nu2(n-2)2u2
What is the minimum energy required to launch a satellite of mass m from the surface of a planet of mass M and radius R in a circular orbit at an altitude of 2R?
5GmM/6R
2GmM/3R
GmM/2R
GmM/2R
The mass of a spaceship is 1000 kg. It is to be launched from the earth's surface out into free space. The value of 'g'and 'R'(radius of earth) are 10 m/s2 and 6400km respectively. The required energy for this work will be;
6.4 x1011 J
6.4 x108 J
6.4 x109 J
6.4 x109 J
Two bodies of masses m and 4 m are placed at a distance r. The gravitational potential at a point on the line joining them where the gravitational field is zero is
-4Gm/r
-6Gm/r
-9Gm/r
-9Gm/r
The variation of acceleration due to gravity g with distance d from centre of the earth is best represented by (R = Earth's radius)
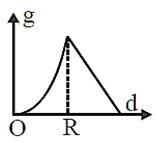
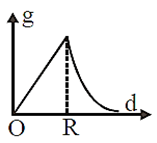
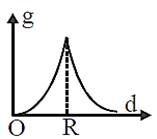

The height at which the acceleration due to gravity becomes g/9 (where g = the acceleration due to gravity on the surface of the earth) in terms of R, the radius of the earth, is
2R
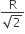
R/2
R/2
