 Multiple Choice Questions
Multiple Choice QuestionsThe number of common tangent to the circles x2+y2-4x-6y-12=0 and x2+y2+6x+18y+26 = 0 is
1
2
3
3
The angle between the lines whose direction cosines satisfy the equations l +m+n=0 and l2 = m2+n2 is
π/3
π/4
π/6
π/6
If PS is the median of the triangle with vertices P(2,1), Q(6,-1) and R (7,3), then equation of the line passing through (1,-1) and parallel to PS is
4x-7y - 11 =0
2x+9y+7=0
4x+7y+3 = 0
4x+7y+3 = 0
Let a,b,c and d be non-zero numbers. If the point of intersection of the lines 4ax +2ay +c= 0 and 5bx +2by +d = 0 lies in the fourth quadrant and is equidistant from the two axes, then
2bc-3ad =0
2bc+3ad =0
2ad-3bc =0
2ad-3bc =0
The x-coordinate of the incentre of the triangle that has the coordinates of mid points of its sides as (0, 1) (1, 1) and (1, 0) is
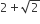
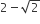
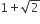
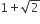
Twenty meters of wire is available for fencing off a flower-bed in the form of a circular sector.Then the maximum area (in sq. m) of the flower-bed, is
30
12.5
10
10
The projections of a vector on the three coordinate axis are 6, - 3, 2 respectively. The direction cosines of the vector are
6, –3, 2
6/5, -3/5, 2/5
6/7, -3/7, 2/7
6/7, -3/7, 2/7
A triangular park is enclosed on two sides by a fence and on the third side by a straight river bank. The two sides having fence are of same length x. The maximum area enclosed by the park is
3x2/2
x3/8
x2/2
x2/2
If (a, a2 ) falls inside the angle made by the lines y =x/2, x >0 and y = 3x, x > 0, then a belongs to
(0,1/2)
(3, ∞)
(1/2, 3)
(1/2, 3)
Let A(2,- 3) and B(- 2,1) be two angular points of AABC. If the centroid of the triangle moves on the line 2x + 3y = 1, then the locus of the angular point C is given by
2x + 3y = 9
2x - 3y = 9
3x + 2y = 5
3x + 2y = 3
