 Multiple Choice Questions
Multiple Choice Questions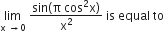
π/2
1
-π
-π
D.
-π
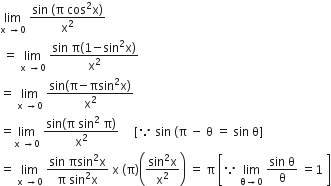
The equation of the tangent to the curve y = x +4/x2, that is parallel to the x-axis, is
y= 0
y= 1
y= 2
y= 2
Let cos (α + β) = 4/5 and let sin (α - β) = 5/13, where 0 ≤α,β ≤ π/4. Then tan 2α is equal to
25/16
56/33
19/12
19/12
The differential equation which represents the family of curves y=c1ec2xe, where c1 and c2 are arbitrary constants, is
y' =y2
y″ = y′ y
yy″ = y′
yy″ = y′
The solution of the differential equation 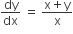 satisfying the condition y (1) = 1 is
satisfying the condition y (1) = 1 is
y = ln x + x
y = x ln x + x2
y = xe(x−1)
y = xe(x−1)
For each t ∈R, let [t] be the greatest integer less than or equal to t. Then
does not exist (in R)
is equal to 0
is equal to 15
is equal to 120
