 Multiple Choice Questions
Multiple Choice QuestionsThe equation of the tangent to the curve y = x +4/x2, that is parallel to the x-axis, is
y= 0
y= 1
y= 2
y= 2
Let cos (α + β) = 4/5 and let sin (α - β) = 5/13, where 0 ≤α,β ≤ π/4. Then tan 2α is equal to
25/16
56/33
19/12
19/12
If 5(tan2x – cos2x) = 2cos 2x + 9, then the value of cos4x is
-7/9
-3/5
1/3
1/3
A.
-7/9
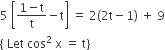
⇒5(1 – t – t2) = t(4t + 7)
⇒ 9t2 + 12t – 5 = 0
⇒ 9t2 + 15t – 3t – 5 = 0
⇒ (3t – 1) (3t + 5) = 0
⇒ t = t/3 as t≠-5/3.
cos2x = 2(1/3)-1 = -1/3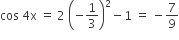
The differential equation which represents the family of curves y=c1ec2xe, where c1 and c2 are arbitrary constants, is
y' =y2
y″ = y′ y
yy″ = y′
yy″ = y′
The solution of the differential equation 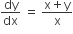 satisfying the condition y (1) = 1 is
satisfying the condition y (1) = 1 is
y = ln x + x
y = x ln x + x2
y = xe(x−1)
y = xe(x−1)
For each t ∈R, let [t] be the greatest integer less than or equal to t. Then
does not exist (in R)
is equal to 0
is equal to 15
is equal to 120
