 Multiple Choice Questions
Multiple Choice QuestionsThere is a circular tube in a vertical plane. Two liquids which do not mix and of densities d1 and d2 are filled in the tube. Each liquid subtends 90o angle at centre. Radius joining their interface makes an angle α with vertical. ratio d1/d2 is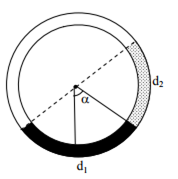
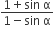
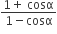


On the heating water, bubbles being formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius R and making a circular contact of radius r with the bottom of the vessel. If r < < R and the surface tension of water is T, value of r just before bubbles detach is (density of water is ρw)
![]()
![]()
![]()
![]()
An open glass tube is immersed in mercury in such a way that a length of 8 cm extends above the mercury level. The open end of the tube is then closed and sealed and the tube is raised vertically up by additional 46 cm. What will be the length of the air column above mercury in the tube now? (Atmospheric pressure = 76 cm of Hg)
16 cm
22 cm
38 cm
38 cm
Water is flowing continuously from a tap having an internal diameter 8 × 10-3 m. The water velocity as it leaves the tap is 0.4 ms-1. The diameter of the water stream at a distance 2 × 10-1 m below the tap is close
to:
7.5 x 10-3 m
9.6x 10-3 m
3.6x 10-3 m
3.6x 10-3 m
A ball is made of a material of density ρ where ρoil < ρ < ρwater with ρoil and ρwater representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position?




The following observations were taken for determining surface tension T of water by the capillary method :
Diameter of capillary, D = 1.25 × 10–2 m rise of water, h = 1.45 × 10–2 m
Using g = 9.80 m/s2 and the simplified relation T = (rhg/2) x103 n/m, the possible error in surface tension is closest to:
2.4%
10%
0.15%
0.15%
A spherical solid ball of volume V is made of a material of density ρ1. It is falling through a liquid of density ρ2(ρ2 <ρ1). Assume that the liquid applies a viscous force on the ball that is proportional to the square of its speed v, i.e., Fviscous = −kv2 (k>0). The terminal speed of the ball is
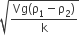

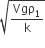
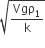
A jar filled with two non-mixing liquids 1 and 2 having densities ρ1 and ρ2 respectively. A solid ball, made of a material of density ρ3, is dropped in the jar. It comes to equilibrium in the position shown in the figure.
Which of the following is true for ρ1, ρ2 and ρ3?
ρ3 < ρ1 < ρ2
ρ1 < ρ3 < ρ2
ρ1 < ρ2 < ρ3
ρ1 < ρ2 < ρ3
A capillary tube (A) is dropped in water. Another identical tube (B) is dipped in a soap water solution.Which of the following shows the relative nature of the liquid columns in the two tubes?




If the terminal speed of a sphere of gold (density = 19.5 kg/m3 ) is 0.2 m/s in a viscous liquid (density = 1.5 kg/m3 ) of the same size in the same liquid.
0.2 m/s
0.4 m/s
0.133 m/s
0.133 m/s
