 Multiple Choice Questions
Multiple Choice QuestionsThe number of integers greater than 6000 that can be formed, using the digits 3,5,6,7 and 8 without repetition, is
216
192
120
120
If m is the AMN of two distinct real numbers l and n (l,n>1) and G1, G2, and G3 are three geometric means between l and n, then 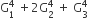 equals
equals
4l2 mn
4lm2n
4 lmn2
4 lmn2
How many different words can be formed by jumbling the letters in the word MISSISSIPPI in which no two S are adjacent?
8 . 6C4 . 7C4
6 . 7 . 8C4
6 . 8 . 7C4
6 . 8 . 7C4
The set S: {1, 2, 3, …, 12} is to be partitioned into three sets A, B, C of equal size. Thus, A ∪ B ∪ C = S, A ∩ B = B ∩ C = A ∩ C = φ. The number of ways to partition S is-
12!/3!(4!)3
12!/3!(3!)4
12!/(4!)3
12!/(4!)3
C.
12!/(4!)3
Number of ways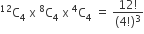
How many ways are there to arrange the letters in the word GARDEN with the vowels in alphabetical order?
120
480
360
360
The number of ways of distributing 8 identical balls in 3 distinct boxes so that none of the boxes is empty is
5
38
38
The greatest integer which divides (p + 1) (p + 2) (p + 3) .... (p + q) for all p E N and fixed q N is
p!
q!
p
q
The number of ways in which the letters of the word ARRANGE can be permuted such that the R's occur together, is
