 Multiple Choice Questions
Multiple Choice QuestionsIf the number of terms in the expansion of 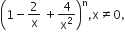 is 28, then the sum of the coefficients of all the terms in this expansion is
is 28, then the sum of the coefficients of all the terms in this expansion is
64
2187
243
243
Statement − 1: For every natural number n ≥ 2 
Statement −2: For every natural number n ≥ 2,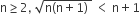
Statement −1 is false, Statement −2 is true
Statement −1 is true, Statement −2 is true, Statement −2 is a correct explanation for Statement −1
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
Statement −1 is true, Statement −2 is true; Statement −2 is not a correct explanation for Statement −1.
If A =  and I =
and I =  , then which one of the following holds for all n ≥ 1, by the principle of mathematical induction
, then which one of the following holds for all n ≥ 1, by the principle of mathematical induction
An = nA – (n – 1)I
An = 2n-1A – (n – 1)I
An = nA + (n – 1)I
An = nA + (n – 1)I
Let S(K) = 1 +3+5+..... (2K-1) = 3+K2. Then which of the following is true?
S(1) is correct
Principle of mathematical induction can be used to prove the formula
S(K) ≠S(K+1)
S(K) ≠S(K+1)
The acceleration of a particle starting from rest moving in a straight line with uniform acceleration is 8 m/s2. The time taken by the particle to move the second metre is
(√2-1)/2 S
(√2+1)/2 S
(1 + √2)S
(√2-1)S
 Short Answer Type
Short Answer Type Multiple Choice Questions
Multiple Choice QuestionsA particle is moving in a straight line. At time t, the distance between the particle from its starting point is given by x = t - 6t2 + t3. Its acceleration will be zero at
t = 1 unit time
t = 2 unit time
t = 3 unit time
t = 4 unit time
