 Multiple Choice Questions
Multiple Choice QuestionsLet A and B be two sets containing four and two elements respectively. Then the number of subsets of the set A x B, each having at least three elements is:
219
256
275
275
Let A and B be two sets containing 2 elements and 4 elements respectively. The number of subsets of A × B having 3 or more elements is
256
220
219
219
Let X = {1, 2, 3, 4, 5}. The number of different ordered pairs (Y, Z) that can be formed such that Y ⊆ X, Z ⊆ X and Y ∩ Z is empty, is
52
35
25
25
Let R be the set of real numbers.
Statement-1 : A = {(x, y) ∈R × R : y - x is an integer} is an equivalence relation on R.
Statement-2 : B = {(x, y) ∈ R × R : x = αy for some rational number α} is an equivalence relation on R.
Statement-1 is true, Statement-2 is true; Statement-2 is a correct explanation for Statement-1.
(2) Statement-1 is true, Statement-2 is true; Statement-2 is not a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is false.
Statement-1 is true, Statement-2 is false.
If A, B and C are three sets such that A ∩ B = A∩ C and A ∪ B = A ∪ C, then
A = B
A = C
B = C
B = C
A die is thrown. Let A be the event that the number obtained is greater than 3. Let B be the event that the number obtained is less than 5. Then P (A ∪ B) is
3/5
0
1
1
Let A and B be two events such that 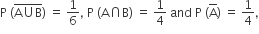 where
where  stands for complement of event A. Then events A and B are
stands for complement of event A. Then events A and B are
equally likely and mutually exclusive
equally likely but not independent
independent but not equally likely
independent but not equally likely
Two sets A and B are as under:
A = {(a-b)∈ RxR:|a-5|<1 and |b-5|<1}
B = {(a,b)∈ Rx R: 4(a-6)2 + 9 (b-5)2 ≤ 36},then
Neither A ⊂ B nor B ⊂ A
B ⊂ A
A ⊂ B
A ∩ B = ∅
On R, the set of real numbers, a relation p is defined as 'ab if and only if 1+ ab> 0'. Tnen,
is an equivalence relation
is reflexive and transitive but not symmetric
is reflexive and symmetric but not transitive
is only symmetric
