 Multiple Choice Questions
Multiple Choice QuestionsIf the standard deviation of the numbers 2, 3, a and 11 is 3.5, then which of the following is true?
3a2−26a+55=0
3a2−32a+84=0
3a2−34a+91=0
3a2−34a+91=0
Let y(x) be the solution of the differential equation 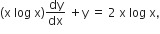 (x ≥1). Then, y (e) is equal to
(x ≥1). Then, y (e) is equal to
e
0
2
2
Let In ∫tan x dx,(n> 1) . I4 + I6 = a tan5x + bx5 + C, where C is a constant of integration, then the ordered pair (a, b) is equal to
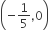
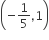


Let the orthocentre and centroid of a triangle be A(–3, 5) and B(3, 3) respectively. If C is the circumcentre of this triangle, then the radius of the circle having line segment AC as diameter, is
Consider the non-constant differentiable function f of one variable which obeys the relation f(x - y ). If f'(0)= p and f(y) . f'(5) = q, then f'(- 5) is
q
