 Multiple Choice Questions
Multiple Choice QuestionsIf radius of 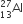 nucleus is estimated to be 3.6 Fermi then the radius
nucleus is estimated to be 3.6 Fermi then the radius  nucleus
nucleus
6 fermi
8 fermi
4 fermi
4 fermi
A nuclear transformation is denoted by X(n, α) 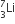 . Which of the following is the nucleus of element X?
. Which of the following is the nucleus of element X?
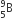
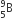
Two spherical conductor B and C having equal radii and carrying equal charges in them repel each other with a force F when kept apart at some distance. A third spherical conductor having same radius as that of B but uncharged brought in contact with B, then brought in contact with C and finally removed away from both. The new force of repulsion, between B and C is
F/4
3F/4
3F/8
3F/8
A nucleus disintegrates into two nuclear parts which have their velocities in the ratio 2:1. The ratio of their nuclear sizes will be
21/3:1
1:31/2
31/2:1
31/2:1
The binding energy per nucleon of deuteron (21H) and helium nucleus (42He) is 1.1 MeV and 7 MeV respectively. If two deuteron nuclei react to form a single helium nucleus, then the energy released is
13.9 MeV
26.9 MeV
23.6 MeV
23.6 MeV
An α-particle of energy 5 MeV is scattered through 180° by a fixed uranium nucleus. The distance of the closest approach is of the order of
1 Å
10−10 cm
10−12 cm
10−12 cm
Which of the following particle when bombards on 65Cu will turn into 66Cu ?
Proton
Neutron
Electron
Alpha particle
8 g of Cu66 undergoes radioactive decay and after 15 minutes only 1 g remains. The half-life, in minutes, is then
15 ln (2) / ln(8)
15 ln (8) / ln (2)
15/8
8/15
For a light nuclei, which of the following relation between the atomic number (Z) and mass number (A) is valid ?
A = Z/2
Z = A
Z = A/2
Z = A2
During β− emission,
a neutron in the nucleus decays emitting an electron
an atomic electron is ejected
an electron already present within the nucleus is ejected
a part of the binding energy of the nucleus is converted into an electron
