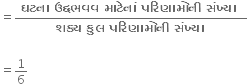જ્યારે એક સમતોલ પાસો ઉછાળવમાં આવે ત્યારે પાસા પર 1, 4 અથવા 5 આવે તે પ્રત્યેક ઘટનાની સંભાવના શોધો.
સમતોલ પાસો ઉછાળવાના પ્રયોગમાં શક્ય સમસંભાવી પરિણામો 1,2,3,4,5 અને 6 છે.
ધારો કેેે પાસાા પર અંક ,આવેતે ઘટના E છેેે, તો E ના ઉદ્દભવ માટેનાંં પરિણામો ફક્ત 1છે.
∴P(E) = P(પાસા પર અંક 1 મળેે)
ધારો કે, પાસા પર અંક 4 આવે તે ઘટના F છે, તો F ના ઉદ્દભવ માટેનાં પરિણામો ફક્ત 1 છે.
∴P(F)=P(પાસા પર અંક 4 મળે)
ધારો, કે પાસા પર અંક 5 આવે તે ઘટના G છે, તો Gના ઉદ્દભવ માટેનાં પરિણામો ફક્ત 1 છે.
∴P(G) = P(પાસા પર અંક 5 મળે)