 Multiple Choice Questions
Multiple Choice QuestionsAt what height from the surface of earth the gravitation potential and the value of g are -5.4 x 107 J kg-2 and 6.0 m/s2 respectively? (Take the radius of the earth as 6400 km)
1600 km
1400 km
2000 km
2600 km
Kepler's third law states that square of the period of revolution (T) of a planet around the sun, is proportional to the third power of average distance r between the sun and planet i.e, T2 =Kr3, here K is constant.
If the masses of the sun and planet are M and m respectively, them as per Newton's law of gravitation force of attraction between them is 
The relation between G and K is described as
GK =4π2
GMK =4π2
K=G
K=G
Two spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body before collision is
2.5 R
4.5 R
7.5 R
1.5 R
If ve is escape velocity and vo is orbital velocity of a satellite for orbit close to the Earth's surface, then these are related by




Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of radius R? (r is measured from the centre of the spherical shell).
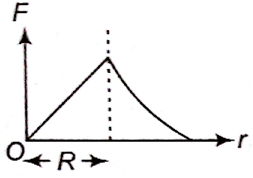



A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass = 5.98 x 1024 kg) have to be compressed to be a black hole?
10-9 m
10-6 m
10-2 m
10-2 m
Dependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by,
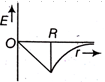
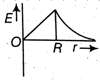
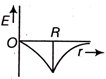
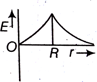
The height at which the weight of a body becomes 1/16th, its weight on the surface of earth (radius R), is
5R
15 R
3R
3R
A geostationary satellite is orbiting the earth at a height of 5R above that surface of the earth, R being the radius of the earth. The time period of another satellite in hours at a height of 2R from the surface of the earth is
5
10


A spherical planet has a mass Mp and diameter Dp. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to
4GMp/Dp2
GMpm/Dp2
GMpm/ Dp2
GMpm/ Dp2
A.
4GMp/Dp2

