Gravitation

At what height from the surface of earth the gravitation potential and the value of g are -5.4 x 10⁷ J kg^-2 and 6.0 m/s² respectively? (Take the radius of the earth as 6400 km)

• 1600 km

• 1400 km

• 2000 km

• 2600 km

Kepler's third law states that square of the period of revolution (T) of a planet around the sun, is proportional to the third power of average distance r between the sun and planet i.e, T² =Kr³, here K is constant.
If  the masses of the sun and planet are M and m respectively, them as per Newton's law of gravitation force of attraction between them is 


The relation between G and K is described as

• GK =4π²

• GMK =4π²

• K=G

• K=G

Two spherical bodies of masses M and 5M and radii R and 2R are released in free space with initial separation between their centres equal to 12 R. If they attract each other due to gravitational force only, then the distance covered by the smaller body before collision is

• 2.5 R

• 4.5 R

• 7.5 R 

• 1.5 R 

If v_e is escape velocity and v_o is orbital velocity of a satellite for orbit close to the Earth's surface, then these are related by

Which one of the following plots represents the variation of the gravitational field on a particle with distance r due to a thin spherical shell of radius R? (r is measured from the centre of the spherical shell).

A black hole is an object whose gravitational field is so strong that even light cannot escape from it. To what approximate radius would earth (mass = 5.98 x 10²⁴ kg) have to be compressed to be a black hole?

• 10^-9 m

• 10^-6 m

• 10^-2 m

• 10^-2 m

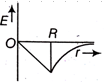
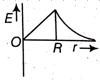
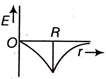
Dependence of intensity of gravitational field (E) of earth with distance (r) from centre of earth is correctly represented by,

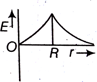
The height at which the weight of a body becomes 1/16th, its weight on the surface of earth (radius R), is

• 5R

• 15 R

• 3R

• 3R

A geostationary satellite is orbiting the earth at a height of 5R above that surface of the earth, R being the radius of the earth. The  time period of another satellite in hours at a height of 2R from the surface of the earth is

• 5

• 10

• 
• 

A spherical planet has a mass M_p and diameter D_p. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity, equal to

• 4GM_p/D_p²

• GM_pm/D_p²

• GM_pm/ D_p²

• GM_pm/ D_p²