 Multiple Choice Questions
Multiple Choice QuestionsA car is negotiating a curved road of radius R. The road is banked at angle θ. The coefficient of friction between the tyres of the car and the road is μs . The maximum safe velocity on this road is,
![]()
![]()
![]()
![]()
A particle of mass m is driven by a machine that delivers a constant power K watts. If the particle starts from rest, the force on the particle at time t is
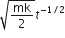



Three blocks A, B, and C of masses 4 kg, 2 kg and 1 kg respectively, are in contact on a 14 N is applied to the 4 kg block, then the contact force between A and B is
2 N
6 N
8 N
8 N
A block A of mass m1 rests on a horizontal table. A light string connected to it passes over a frictionless pulley at the edge of the table and from its other end, another block B of mass m2 is suspended. The coefficient of kinetic friction between the block and the table is  . When the block A is sliding on the table, the tension in the string is
. When the block A is sliding on the table, the tension in the string is
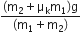
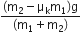
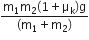
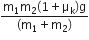
A stone is dropped from a height h. It hits the ground with a certain momentum p. If the same stone is dropped from a height 100% more than the previous height, the momentum when it hits the ground will change by
68%
41%
200%
200%
A car of mass m is moving on a level circular track of radius R. If  represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by
represents the static friction between the road and tyres of the car, the maximum speed of the car in circular motion is given by




Three masses are placed on the x- axis: 300g at origin, 500g at x = 40 cm and 400 g at x = 70 cm. The distance of the centre of mass from the origin is
40 cm
45 cm
50 cm
50 cm
A system consists of three masses m1, m2 and m3 connected by a string passing over a pulley P. The mass m1 hangs freely and m2 and m3 are on a rough horizontal table (the coefficient of friction = μ). the pulley is frictionless and of negligible mass. The downward acceleration of mass m1 is,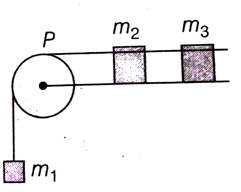
![]()
![]()
![]()
![]()
A solid cylinder of mass 50 kg and radius 0.5 m is free to rotate about the horizontal axis. A massless string is wound around the cylinder with one end attached to it and other hanging freely. Tension in the string required to produce an angular acceleration of 2 rev/s2 is,
25 N
50 N
78.5 N
78.5 N
The ratio of the accelerations for a solid sphere (mass m and radius R) rolling down an incline of angle  without slipping and slipping down the incline without rolling is,
without slipping and slipping down the incline without rolling is,
5:7
2:3
2:5
2:5
