 Multiple Choice Questions
Multiple Choice QuestionsTwo non-mixing liquids of densities 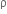 and n
and n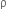 (n >1) are put in a container. The height of each liquid is h. a solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL (p<1) in the denser liquid. The density d is equal to,
(n >1) are put in a container. The height of each liquid is h. a solid cylinder of length L and density d is put in this container. The cylinder floats with its axis vertical and length pL (p<1) in the denser liquid. The density d is equal to,
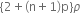

{1+(n-1)p}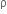
{1+(n-1)p}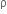
The wind with speed 40 m/s blows parallel to the roof of a house. The area of the roof is 250m2. Assuming that the pressure inside the house is atmospheric pressure, the force exerted by the wind on the roof and the direction of the force will be( pair = 1.2 kg/m3)
4.8 x 105 N, downwards
4.8 x105 N , upwards
2.4 x 105 N , upwards
2.4 x 105 N , upwards
A certain number of spherical drops of a liquid of radius r coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
Energy = 4VT ![]() is released.
is released.
Energy = 3VT![]() is absorbed
is absorbed
Energy = 3 VT ![]() is released
is released
Energy is neither absorbed nor released.
The wettability of a surface by a liquid depends primarily on
viscosity
surface tension
density
density
If dimensions of critical velocity vc of a liquid flowing through a tube are expressed as  are the coefficient of viscosity of liquid, density of liquid and radius of the tube respectively, then the values of x, y and z are given by
are the coefficient of viscosity of liquid, density of liquid and radius of the tube respectively, then the values of x, y and z are given by
1,-1,-1
-1,-1,1
-1,-1,-1
-1,-1,-1
Water rises to a height 'h' in a capillary tube. If the length of capillary tube above the surface of water is made less than 'h' then
water rises upto the tip of the capillary tube and then starts overflowing like a fountain
water rises upto the top of capillary tube and stays there without overflowing
water rises upto a point little below the top and stays there
water rises upto a point little below the top and stays there
A U tube with both ends open to the atmosphere is partially filled with water. Oil, which is immiscible with water, is poured into one side until it stands at a distance of 10 mm above the water level on the other side. Meanwhile, the water rises by 65 mm from its original level (see diagram). The density of the oil is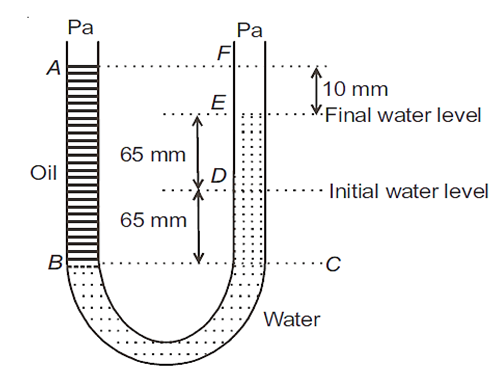
650 kg m–3
425 kg m–3
800 kg m–3
800 kg m–3
A steam of a liquid of density ρ flowing horizontally with speed v rushes out of a tube of radius r and hits a vertical wall nearly normally. Assuming that the liquid does not rebound from the wall, the force exerted on the wall by the impact of the liquid is given by
πrρv
πrρv2
πr2ρv
πr2ρv2
A wide hose pipe is held horizontally by a fireman. It delivers water through a nozzle at one litre per second. On increasing the pressure. this increases to two litres per second. The firman has now to
push forward twice as hard
push forward four times as hard
push backward four times as hard
push backward twice as hard
A liquid is allowed into a tube of truncated cone shape. Identify the correct statement from the following.
The speed is high at the wider end and low at the narrow end
The speed is low at the wider end and high at the narrow end.
The speed is same at both ends in a streamline flow.
The liquid flows with the uniform velocity in the tube.
