 Multiple Choice Questions
Multiple Choice QuestionsA body of mass 1 kg begins to move under the action of a time dependent force F = ![]() N, where
N, where ![]() are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
(2t2 + 4t4) W
(2t3 + 3 t4) W
(2t3 + 3t5) W
(2t + 3t3)W
If the velocity of a particle is v = At + Bt2, where A and B are constants, then the distance travelled by it between 1 s and 2 s is,
3A + 7B
![]()
![]()
![]()
A particle moves so that its position vector is given by r = cos ![]() where
where ![]() is a constant. Which of the following is true?
is a constant. Which of the following is true?
velocity and acceleration both are parallel to r
velocity is perpendicular to r and acceleration is directed towards the origin
velocity is perpendicular to r and acceleration is directed away from the origin
velocity and acceleration both are perpendicular to r
A particle of unit mass undergoes one-dimensional motion such that its velocity according to
V(x) = βx-2n where β and n are constants and x is the position of the particle. The acceleration of the particle as a function of x is given by
-2nβ2 x-2n-1
-2nβ2 x-4n-1
-2β x-2n+1
-2β x-2n+1
What is the minimum velocity with which a body of mass m must enter a vertical loop of radius R so that it can complete the loop?




A particle of mass 10 g moves along a circle of radius 6.4 cm with a constant tangential acceleration. What is the magnitude of this acceleration, if the kinetic energy of the particle becomes equal to 8 x 10-4 J by the end of the second revolution after the beginning of the motion?
0.15 m/s2
0.18 m/s2
0.2 m/s2
0.2 m/s2
A projectile is fired from the surface of the earth with a velocity of 5 m/s and angle  with the horizontal. Another projectile fired from another planet with a velocity of 3 m/s at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is,
with the horizontal. Another projectile fired from another planet with a velocity of 3 m/s at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is,
3.5
5.9
16.3
16.3
A balloon with mass m is descending down with an acceleration a (where a <g). How much mass should be removed from it so that it starts moving up with an acceleration a?
![]()
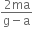
![]()
![]()
The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
A particle has initial velocity (2i+3j) and acceleration (0.31i +0.2j). The magnitude of velocity after 10 s will be
 units
units
 units
units
5 units
5 units
