From a disc of radius R and mass M, a circular hole of diameter R, whose rim passes through the centre is cut. What is the moment of inertia of the remaining part of the disc, about a perpendicular axis, passing through the centre?

• 13 MR²/32

• 11MR²/32

• 9MR²/32

• 15MR²/32

A disc and a sphere of the same radius but differnt masses roll off two inclined planes of the same altitude and length. which one of the two objects gets to the bottom of the plane first?

• Sphere

• Both reach at the same time

• Depends on their masses

• Disc

3.

A uniform circular disc of radius 50 cm at rest is free to turn about an axis which is perpendicular to its plane and passes through its centre. It is subjected  to a torque which produces a constant angular acceleration of 2.0 rad/sec². It's net acceleration in m/s² at the end of 2.0 s is a approximately.

• 7.0

• 6.0

• 3.0

• 8.0

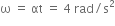
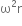
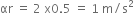
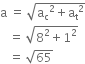
A rod of weight w is supported by two parallel knife edges A and B and is in equilibrium in a horizontal position. The knives are at distance d from each other. The centre of mass of the rod is at distance x from A. The normal reaction on A is

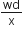
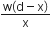
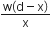
A mass m moves in a circle on a smooth horizontal plane with velocity v_o at a radius R_o. The mass is attached to a string which passes through a smooth hole in the plane as shown.

The tension in the string is increased gradually and finally m moves in a circle in a circle of radius R_o/2. The final values of the kinetic energy is

• mv₀²

• 1/4mv_o²

• 2mv_o²

• 2mv_o²

Three identical spherical shells, each of mass m and radius r are placed as shown in the figure. Consider an axis XX^', which is touching to two shells and passing through the diameter of the third shell. Moment of inertia of the system consisting of these three spherical shells about XX' axis is

• 11/5 mr²

• 3 mr²

• 16/5 mr²

• 16/5 mr²

A circular platform is mounted on the frictionless vertical axle. Its radius R =2 m and its moment of inertia about the axle is 200 kg m². It is initially at rest. A 50 kg man stands on the edge of the platform and begins to walk along the edge at the speed of 1 ms^-1 relative to the ground. Time taken by the man to complete one revolution is

• π sec

• 3π/2 sec

• 2π sec

• 2π sec

The moment of inertia of a uniform circular disc is maximum about an axis perpendicular to the disc and passing through

• B

• C

• D

• D

When a string is divided into three segments of length l₁, l₂, and l₃ the fundamental frequencies of these three segments are v₁, v₂, and v₃ respectively. The original fundamental frequency (v) of the string is

• 

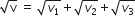
• v = v₁ +v₂ +v₃

• 
• 

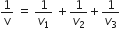
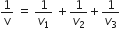
When a mass is rotating in a plane about a fixed point, its angular momentum is directed along

• a line perpendicular to the plane of rotation

• the line making an angle of 45^o to the plane of rotation

• the radius

• the radius