Units and Measurement

If energy (E), velocity (v) and time (T) are chosen  as the fundamental quantities, the dimensional formula of surface tension will be

• [Ev^-2T^-1]

• [Ev^-1T^-2]

• [Ev^-2T^-2]

• [Ev^-2T^-2]

The dimensions of  are

• [L^1/2 T^-1/2]

• [L^-1T]

• [LT^-1]

• [LT^-1]

If force (F), velocity (v) and time (T) are taken as fundamental units, then the dimensions of mass are

• [FvT^-1]

• [FvT^-2]

• [Fv^-1T^-1]

• [Fv^-1T^-1]

In an experiment, four quantities a,b, c and d are measured with percentage error 1%, 2%, 3% and 4% respectively. Quantity P is calculated as follows:

P = 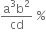, error in P is

• 14 %

• 10 %

• 7 %

• 7 %

The dimensions of  are

• [L^-1T]

• [LT^-]

• [L-^1/2 T^1/2]

• [L-^1/2 T^1/2]

The cylindrical tube of a spray pump has radius R, one end of which has n fine holes, each of radius r. if the speed of the liquid in the tube is v, the speed of the ejection of the liquid through the holes is

• vR²/n²r²

• vR²/nr²

• vR²/n³r²

• vR²/n³r²

The density of material in CGS system of units is 4g/ cm².In a system of units in which unit of lengths is 10 cm and unit of mass is 100 g, the value of density of material will be 

• 0.4

• 40

• 400

• 400

The dimension of 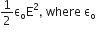, is permittivity of free space and E is electric field is 

• [ML²T^-2]

• [ML^-1T^-3]

• [ML²T^-1]

• [ML²T^-1]

If the dimensions of a physical quantity are given by M^a L^b T^c, the physical quantity will be 

• pressure if a = 1, b = -1, c= 2

• velocity if a = 1, b = 1, c = -2

• acceleration if a = 1, b = 1, c =-2

• acceleration if a = 1, b = 1, c =-2

If the error in the measurement of radius of sphere is 2%, then the error in the determination of volume of the sphere will be

• 4%

• 6%

• 8%

• 8%