 Multiple Choice Questions
Multiple Choice QuestionsGiven the value of rydberg constant is 10 m-1, the wave number of the last line of the Balmer series in hydrogen spectrum will be:
0.5 x 107 m-1
0.25 x 107 m-1
2.5 x107 m-1
2.5 x107 m-1
The ratio of escape velocity at earth (Ve) to the escape velocity at a planet (vp) whose radius and mean density are twice as that of earth is,
1: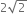
1:4
1:
1:
Consider 3rd orbit of He+ (Helium), using non-relativistic approach, the speed of electron in this orbit will be (given K= 9 x 109 constant, Z=2 and h (Planck's constant = 6.6 x 10-34 Js-1
2.92 x 106 m/s
1.46 x 106 m/s
0.73 x 106 m/s
0.73 x 106 m/s
A proton carrying 1 MeV kinetic energy is moving in a circular path of radius R in the uniform magnetic field. What should be the energy of an alpha particle to describe a circle of the same radius in the same field.
2 MeV
1 MeV
0.5 MeV
0.5 MeV
The transition from the state n = 3 to n=1 in a hydrogen-like atom results in ultraviolet radiation. Infrared radiation will be obtained in the transition from.
2→ 1
3 →2
4 → 2
4 → 2
An electron in hydrogen atom first jumps from third excited state to second excited state and then from second excited to the first excited state. The ratio of the wavelengths λ1:λ2 emitted in the two cases is
7/5
27/20
27/5
27/5
An electron of a stationary hydrogen atom passes from the fifth energy level to ground level. The velocity that the atom acquired as a result of photon emission will be
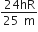
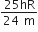
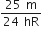
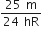
Hydrogen atom in ground state is excited by a monochromatic radiation of 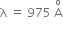 . The number of spectral lines in the resulting spectrum emitted will be,
. The number of spectral lines in the resulting spectrum emitted will be,
3
2
6
6
A certain mass of hydrogen is changed to helium the process of fusion. The mass defect in fusion reaction is 0.02866 u. The energy liberated per u is (given 1 u =931 MeV)
2.67 MeV
26.7 MeV
6.675 MeV
6.675 MeV
