 Multiple Choice Questions
Multiple Choice QuestionsA non -conducting ring of radius 0.5m carries a total charge of 1.11 x 10-10 C distributed non-uniformly on its circumference producing on its circumference on the electric field. E everywhere is space.
The value of the line integral (l = 0 being centre of ring) in volts is
+2
-1
-2
zero
a potentiometer wire is 100 cm long and a constant potential difference is maintained across it. Two cells are connected in series first to support one another and then in opposite direction. The balance points are obtained at 50 cm and 10 cm from the positive end of the wire in the two cases. The ratio of emf is,
5:4
3:4
3:2
3:2
A square loop of ABCD carrying a current i, is placed near and coplanar with a long straight conductor XY carrying a current I, the net force on the loop will be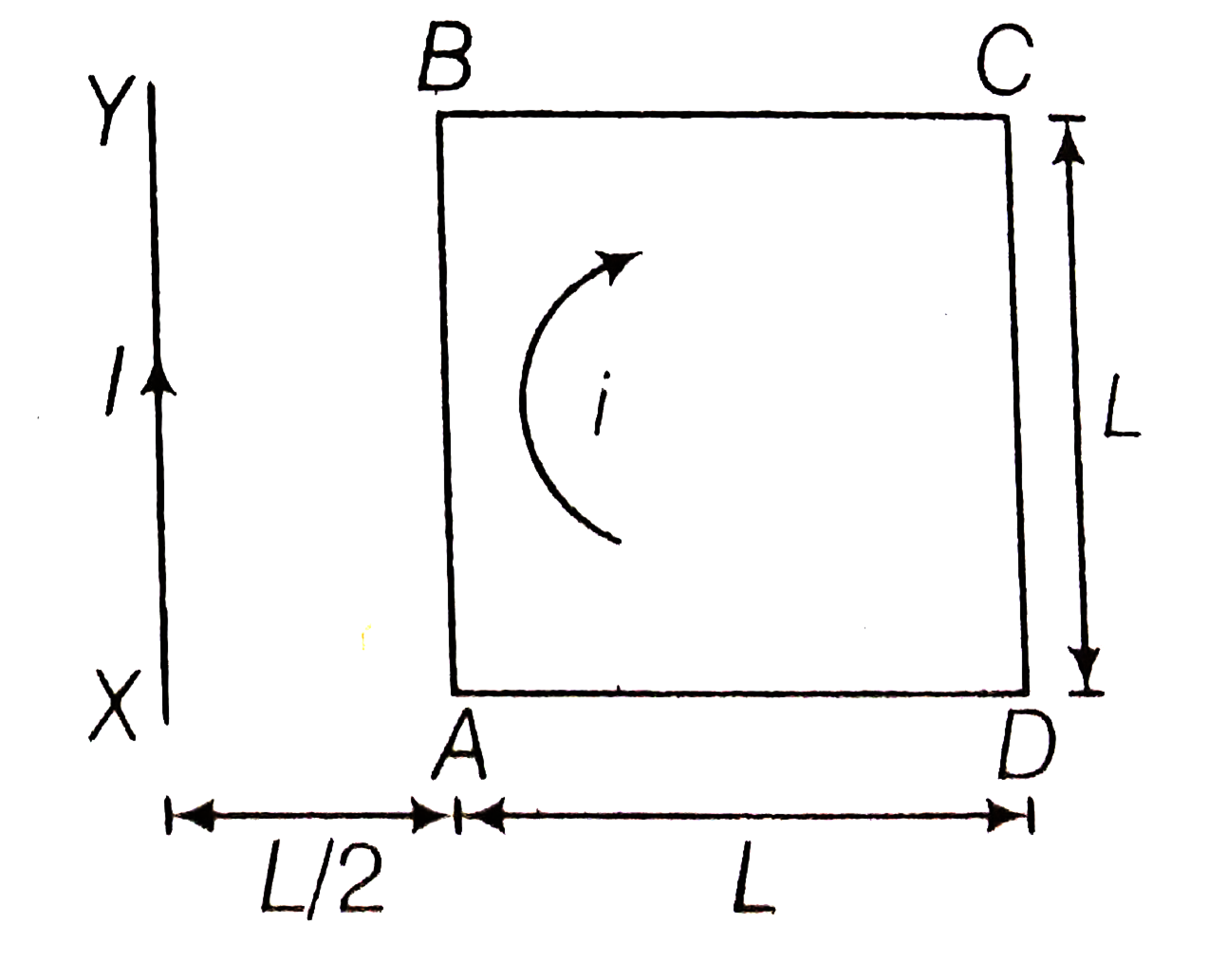

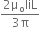


A, B and C are voltmeters of resistance R, 1.5 R and 3R respectively as shown in the figure. When some potential difference is applied between X and Y, the voltmeter readings are VA, VB and Vc respectively then,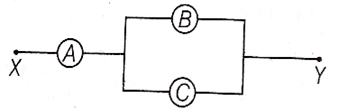
VA =VB =Vc
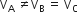
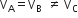
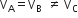
The power dissipated in the circuit shiwn in the figure is 30 Watt. The value of R is
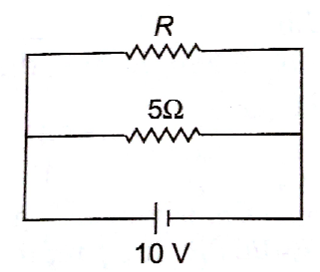
20 Ω
15Ω
10Ω
10Ω
A cell having an emf and internal resistance r is connected across a variable external resistance R. As the resistance R is increased, the plot of potential difference V across R is given by




In an electrical circuit R, L, C and AC voltage source are all connected in series when L is removed from the circuit, the phase difference between the voltage and the current in the circuit is π/3. If instead, Cis removed from the circuit, the phase difference is again π/3. The power factor of the circuit is
1/2
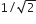
1
1
A millivoltmeter of 25 mV range is to be converted into an ammeter of 25 A range. The value (in ohm) of necessary shunt will be
0.001
0.01
1
1
A ring is made of wire having a resistance Ro = 12Ω. Find the points A and B, as shown in the figure, at which a current carrying conductor should be connected so that the resistance R of the subcircuit between these points is equal to 8/3Ω

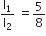
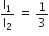
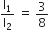
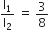
The resistances in the two arms of the meter bridge are 5 ohm and R ohm, respectively. When the resistance R is shunted with an equal resistance, the new balance point is at 1.6 l1. The resistance R is,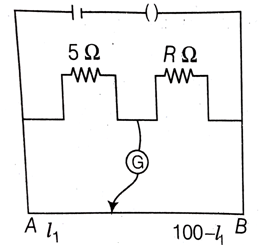
10 ohm
15 ohm
20 ohm
20 ohm
