 Short Answer Type
Short Answer TypeWrite the principal value of 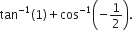
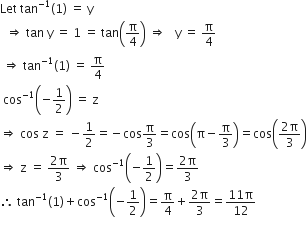
 Long Answer Type
Long Answer TypeA school wants to award its students for the values of Honesty, Regularity and Hard work with a total cash award of Rs 6,000. Three times the award money for Hard work added to that given for honesty amounts to Rs 11,000. The award money given for Honesty and Hard work together is double the one given for Regularity. Represent the above situation algebraically and find the award money for each value, using matrix method. Apart from these values, namely, Honesty, Regularity and Hard work, suggest one more value which the school must include for awards.
