1.

If A is a 3 × 3 invertible matrix, then what will be the value of k if det(A^–1) = (det A)^k.

Determine the value of the constant ‘k’ so that the function  is continuous at x = 0.

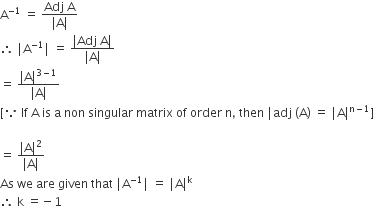
If a line makes angles 90° and 60° respectively with the positive directions of x and y axes, find the angle which it makes with the positive direction of the z-axis.

Show that all the diagonal elements of a skew symmetric matrix are zero.

The volume of a sphere is increasing at the rate of 3 cubic centimetres per second. Find the rate of increase of its surface area, when the radius is 2 cm.

Show that the function f(x) = 4x³ – 18x² + 27x – 7 is always increasing on R.

Prove that 

Using properties of determinants, prove that 

Let find a matrix D such that CD – AB = O.