 Long Answer Type
Long Answer Type(a) (i) 'Two independent monochromatic sources of light cannot produce a sustained interference pattern'. Give reason.
(ii) Light waves each of amplitude 'a' and frequency 'ω', emanating from two coherent light sources superpose at a point. If the displacements due to these waves is given by y1 = a cos ωt and y2 = a cos(ωt + ϕ) where ϕ is the phase difference between the two, obtain the expression for the resultant intensity at the point.
(b) In Young's double slit experiment, using monochromatic light of wavelength λ, the intensity of light at a point on the screen where path difference is λ, is K units. Find out the intensity of light at a point where path difference is λ/3.
(a)
(i) The condition for the sustained interference is that both the sources must be coherent (i.e. they must have the same wavelength and the same frequency, and they must have the same phase or constant phase difference).
Two sources are monochromatic if they have the same frequency and wavelength. Since they are independent, i.e. they have different phases with irregular difference, they are not coherent sources.
ii) 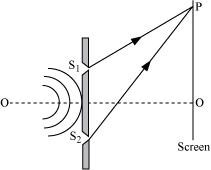
Let the displacement of the waves from the sources S1 and S2 at point P on the screen at any time t be given by:
y1 = a cos ωt
y2 = a cos (ωt + Φ)
where, Φ is the constant phase difference between the two waves.
By the superposition principle, the resultant displacement at point P is given by:
y = y1 + y2
y = a cos ωt + a cos (ωt + Φ)
=2 a[cos cos ![]()
y = 2 acos ![]() cos
cos ![]() ... (i)
... (i)
![]() ... (2)
... (2)
Then, equation (i) becomes:
y = A cos (ωt+![]()
Now, we have:
![]() ... (3)
... (3)
The intensity of light is directly proportional to the square of the amplitude of the wave. The intensity of light at point P on the screen is given by:
I = 4 a2 cos2 (![]() ) ... (4)
) ... (4)
(b) Wavelength of monochromatic light = ![]()
Path difference = ![]() .
.
So, phase difference,![]()
Intensity of light = K units
Intensity is given by, ![]()
When path difference is ![]()
Intensity of light, I’=![]() =
= ![]()
![]()
(a) How does one demonstrate, using a suitable diagram, that unpolarized light when passed through a Polaroid gets polarized?
(b) A beam of unpolarized light is incident on a glass-air interface. Show, using a suitable ray diagram, that light reflected from the interface is totally polarized, when μ = tan iB, where μ is the refractive index of glass with respect to air and iB is the Brewster's angle.(a) State briefly the processes involved in the formation of p-n junction explaining clearly how the depletion region is formed.
(b) Using the necessary circuit diagrams, show how the V-I characteristics of a p-n junction are obtained in
(i) Forward biasing
(ii) Reverse biasing
How these characteristics are made use in rectification?
(a) Differentiate between three segments of a transistor on the basis of their size and level of doping.
(b) How is a transistor biased to be in active state?
(c) With the help of necessary circuit diagram, describe briefly how n-p-n transistor in CE configuration amplifies a small sinusoidal input voltage. Write the expression for the ac current gain.