Consider the following relations:
R = {(x, y)| x, y are real numbers and x = wy for some rational number w}; S = {(m/p, p/q)| m, n, p and q are integers such that n, q ≠ 0 and qm = pn}. Then

• R is an equivalence relation but S is not an equivalence relation

• neither R nor S is an equivalence relation

• S is an equivalence relation but R is not an equivalence relation

• S is an equivalence relation but R is not an equivalence relation

The Number of complex numbers z such that |z– 1| = |z + 1| = |z – i| equals 

• 0

• 1

• 2

• 2

If α and β are the roots of the equation x² – x +1 =0, then α²⁰⁰⁹ + β²⁰⁰⁹ =

• -2

• -1

• 1

• 1

A person is to count 4500 currency notes. Let a denote the number of notes he counts in the nth minute. If a₁ = a₂ = ... = a₁₀ = 150 and a₁₀, a₁₁, ...are in an A_P with common difference -2, then the time taken by him to count all notes is

• 24 min

• 34 min

• 125 min

• 125 min

The equation of the tangent to the curve y = x +4/x², that is parallel to the x-axis, is

• y= 0

• y= 1

• y= 2 

• y= 2 

Let p(x) be a function defined on R such that 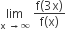 = 1, p'(x)  p'(1-x),for all x∈[0,1] p(0) = 1 and p(1) = 41. Then  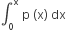equals

• √41

• 21

• 41

• 41

Let S be a non empty subset of R. Consider the
following statement:
P: There is a rational number x∈S such that x > 0.
Which of the following statements is the negation of the statement P?

• There is a rational number x∈S such that x ≤ 0.

• There is no rational number x∈ S such that x≤0.

• Every rational number x∈S satisfies x ≤ 0.

• Every rational number x∈S satisfies x ≤ 0.

Let cos (α + β) = 4/5 and let sin (α - β) = 5/13, where 0 ≤α,β ≤ π/4. Then tan 2α is equal to

• 25/16

• 56/33

• 19/12

• 19/12

For two data sets, each of size 5, the variances are given to be 4 and 5 and the corresponding means are given to be 2 and 4, respectively. The variance of the combined data set is

• 5/2

• 11/2

• 6

• 6

For a regular polygon, let r and R be the radii of the inscribed and the circumscribed circles. A false statement among the following is

• there is a regular polygon with r/R = 1/2

• there is a regular polygon with 

• there is a regular polygon with r/R = 2/3

• there is a regular polygon with r/R = 2/3