 Multiple Choice Questions
Multiple Choice QuestionsThe equation esinx-e-sinx -4 = 0 has
infinite number of real roots
No real root
exactly one real root
exactly one real root
Statement 1: The sum of the series 1 + (1 + 2 + 4) + (4 + 6 + 9) + (9 + 12 + 16) + ...... + (361 + 380 +400) is 8000.
Statement 2: 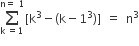 , for any natural number n.
, for any natural number n.
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
The negation of the statement “If I become a teacher, then I will open a school” is
I will become a teacher and I will not open a school
Either I will not become a teacher or I will not open a school
Neither I will become a teacher nor I will open a school
Neither I will become a teacher nor I will open a school
Statement I An equation of a common tangent to the parabola 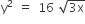 and the ellipse 2x2 +y2 =4 is
and the ellipse 2x2 +y2 =4 is 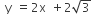 .
.
Statement II If the line 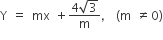 is a common tangent to the parabola
is a common tangent to the parabola 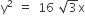 and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
and the ellipse 2x2 +y2 =4, then m satisfies m4 +2m2 =24
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
If n is a positive integer, then 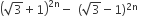 is
is
an irrational number
an odd positive integer
an even positive integer
an even positive integer
If 100 times the 100th term of an AP with non zero common difference equals the 50 times its 50th term, then the 150th term of this AP is
–150
150
times its 50th term
times its 50th term
In a ∆PQR, if 3 sin P + 4 cos Q = 6 and 4 sin Q + 3 cos P = 1, then the angle R is equal to
5π/6
π/6
π/4
π/4
An equation of a plane parallel to the plane x – 2y + 2z – 5 = 0 and at a unit distance from the origin is
x – 2y + 2z – 3 = 0
x – 2y + 2z + 1 = 0
x – 2y + 2z – 1 = 0
x – 2y + 2z – 1 = 0
If the line 2x + y = k passes through the point which divides the line segment joining the points (1, 1) and (2, 4) in the ratio 3 : 2, then k equals
29/5
5
6
6
Let x1, x2, ......, xn be n observations, and let  be their arithmetic mean and σ2 be their variance.
be their arithmetic mean and σ2 be their variance.
Statement 1: Variance of 2x1, 2x2, ......, 2xn is 4 σ2.
Statement 2: Arithmetic mean of 2x1, 2x2, ......, 2xn is 4 .
.
Statement 1 is false, statement 2 is true
Statement 1 is true, statement 2 is true; statement 2 is a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1
Statement 1 is true, statement 2 is true; statement 2 is not a correct explanation for statement 1