If X = {4ⁿ - 3n-1 : n ε N} and Y = {9(n-1):n εN}; where N is the set of natural numbers,then X U Y is equal to

• N

• Y-X

• X

• X

If z is a complex number such that |z|≥2, then the minimum value of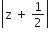

• is equal to 5/2

• lies in the interval (1,2)

• is strictly greater than 5/2

• is strictly greater than 5/2

If a ε R and the equation - 3(x-[x]2 + 2(x-[x] +a² = 0(where,[x] denotes the greatest integer ≤ x) has no  integral solution, then all possible value of  lie in the interval

• (-1,0) ∪ (0,1)

• (1,2)

• (-2,-1)

• (-∞,-2) ∪ (2, ∞)

Let α and β be the roots of equation px² +qx r =0 p ≠0. If p,q and r are in AP and 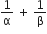 = 4, then the value of |α- β| is

If the coefficients of x³ and x⁴ in the expansion of (1+ax+bx²)(1-2x)¹⁸ in powers of x are both zero, then (a,b) is equal to

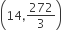
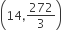
The angle between the lines whose direction cosines satisfy the equations l +m+n=0 and l² = m²+n² is

• π/3

• π/4

• π/6

• π/6

Three positive numbers form an increasing GP. If the middle term in this GP is doubled, then new numbers are in AP. Then, the common ratio of the GP is

• π/2

• 1

• -π

• -π

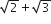
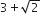
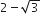
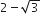
If (10)⁹ +2 (11)²(10)⁷ + .....+10 (11)⁹ = K(10)⁹, then k is equal to

• 121/10

• 441/100

• 100

• 100

If PS is the median of the triangle with vertices P(2,1), Q(6,-1) and R (7,3), then equation of the line passing through (1,-1) and parallel to PS is

• 4x-7y - 11 =0

• 2x+9y+7=0

• 4x+7y+3 = 0

• 4x+7y+3 = 0