 Multiple Choice Questions
Multiple Choice QuestionsIf X = {4n - 3n-1 : n ε N} and Y = {9(n-1):n εN}; where N is the set of natural numbers,then X U Y is equal to
N
Y-X
X
X
D.
X
We have X = {4n - 3n-1 : n ε N}
X = {0,9,54,243,.....} [put n = 1,2,3....]
Y = {9(n-1):n ε N}
Y = {0,9,18,27,......}[Put n = 1,2,3....]
It is clear that
X ⊂ Y
Therefore, X U Y = Y
If z is a complex number such that |z|≥2, then the minimum value of 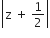
is equal to 5/2
lies in the interval (1,2)
is strictly greater than 5/2
is strictly greater than 5/2
If a ε R and the equation - 3(x-[x]2 + 2(x-[x] +a2 = 0(where,[x] denotes the greatest integer ≤ x) has no integral solution, then all possible value of lie in the interval
(-1,0) ∪ (0,1)
(1,2)
(-2,-1)
(-∞,-2) ∪ (2, ∞)
Let α and β be the roots of equation px2 +qx r =0 p ≠0. If p,q and r are in AP and 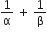 = 4, then the value of |α- β| is
= 4, then the value of |α- β| is




If the coefficients of x3 and x4 in the expansion of (1+ax+bx2)(1-2x)18 in powers of x are both zero, then (a,b) is equal to
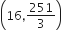
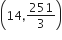
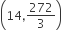
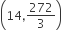
The angle between the lines whose direction cosines satisfy the equations l +m+n=0 and l2 = m2+n2 is
π/3
π/4
π/6
π/6
Three positive numbers form an increasing GP. If the middle term in this GP is doubled, then new numbers are in AP. Then, the common ratio of the GP is
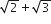
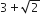
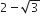
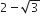
If (10)9 +2 (11)2(10)7 + .....+10 (11)9 = K(10)9, then k is equal to
121/10
441/100
100
100
If PS is the median of the triangle with vertices P(2,1), Q(6,-1) and R (7,3), then equation of the line passing through (1,-1) and parallel to PS is
4x-7y - 11 =0
2x+9y+7=0
4x+7y+3 = 0
4x+7y+3 = 0
