The sum of all real values of x satisfying the equation
 is:

• 3

• -4

• 6

• 6

If all the words (with or without meaning) having five letters, formed using the letters of the word SMALL and arranged as in a dictionary; then the position of the word SMALL is:

• 46^th

• 59^th

• 52^nd

• 52^nd

If the number of terms in the expansion of 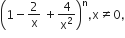 is 28, then the sum of the coefficients of all the terms in this expansion is

• 64

• 2187

• 243

• 243

If the 2^nd, 5^th and 9th terms of a non-constant A.P. are in G.P., then the common ratio of this G.P. is:

• 8/5

• 4/3

• 1

• 1

If the sum of the first ten terms of the series,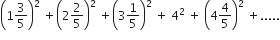

is 16/5 m, the m is equal to

• 102

• 101

• 100

• 100

Let  then log p is equal to 

• 2

• 1

• 1/2

• 1/2

A man is walking towards a vertical pillar in a straight path, at a uniform speed. At a certain point A on the path, he observes that the angle of elevation of the top of the pillar is 30^o. After walking for 10 minutes from A in the same direction, at a point B, he observes that the angle of elevation of the top of the pillar is 60^o. Then the time taken (in minutes) by him, from B to reach the pillar, is:

• 6

• 10

• 20

• 20

If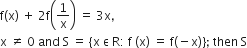 

• is an empty set

• contains exactly one element.

• contains exactly two elements.

• contains exactly two elements.

A value of θ for which  is purely imaginary is

• π/3

• π/6

• 
• 

If A =  and A adj A = AA^T, then 5a +b is equal to

• -1

• 5

• 4

• 4