 Multiple Choice Questions
Multiple Choice QuestionsSTATEMENT – 1
Two particles moving in the same direction do not lose all their energy in a completely inelastic collision.
STATEMENT – 2
Principle of conservation of momentum holds true for all kinds of collisions.
The statement I is True, Statement II is False.
The statement I is True, Statement II is True; Statement II is a correct explanation for Statement I.
The statement I is True, Statement II is True; Statement II is not the correct explanation for Statement I.
The statement I is True, Statement II is True; Statement II is not the correct explanation for Statement I.
A particle is moving with velocity,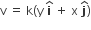 where K is a constant. The general equation for its path is
where K is a constant. The general equation for its path is
y = x2 + constant
y2 = x + constant
xy = constant
xy = constant
The figure shows the position –time (x – t) graph of one–dimensional motion of a body of mass 0.4 kg. The magnitude of each impulse is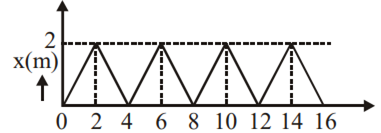
0.4 (Ns)
0.8 Ns
1.6 Ns
1.6 Ns
The respective number of significant figures for the numbers 23.023, 0.0003 and 2.1 × 10–3 are
5,1,2
5,1,5
5,5,2
5,5,2
A point p moves in counter -clockwise direction on a circular path as shown in the figure. The movement of P is such that it sweeps out the length s = t3 + 5, where s is metre and t is in second. The radius of the path is 20 m. The acceleration of P when t =2 s is nearly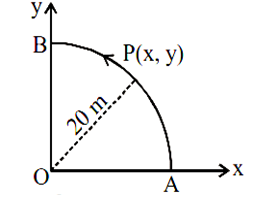
13 ms-2
12 ms-2
7.2 ms-2
7.2 ms-2
Two fixed frictionless inclined planes making an angle 30° and 60° with the vertical are shown in the figure. Two blocks A and B are placed on the two planes. What is the relative vertical acceleration of A with respect to B?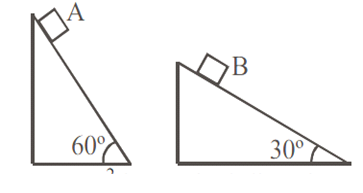
4.9 ms-2 in horizontal direction
9.8 ms-2 in vertical direction
zero
zero
For a particle in uniform circular motion, the acceleration an at  point P (R, θ) on the circle of radius R is (Here θ is measured from the x–axis)
point P (R, θ) on the circle of radius R is (Here θ is measured from the x–axis)
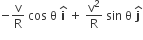
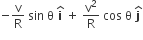
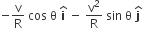
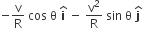
A small particle of mass m is projected at an angle θ with the x–axis with an initial velocity v0 in the x–y plane as shown in the figure. At a time t<vosin/g, the angular momentum of the particle is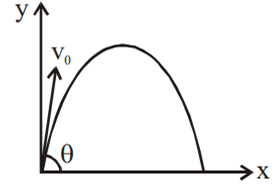


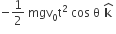
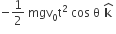
A ball is made of a material of density ρ where ρoil < ρ < ρwater with ρoil and ρwater representing the densities of oil and water, respectively. The oil and water are immiscible. If the above ball is in equilibrium in a mixture of this oil and water, which of the following pictures represents its equilibrium position?




A diatomic ideal gas is used in a Carnot engine as the working substance. If during the adiabatic expansion part of the cycle the volume of the gas increases from V to 32 V,the efficiency of the engine is
0.5
0.75
0.99
0.99