The emission spectrum of hydrogen discovered first and the region of the electromagnetic spectrum in which it belongs, respectively are

• Lyman, ultraviolet

• Lyman, visible

• Balmer, ultraviolet

• Balmer, visible

As per de-Broglie's formula a macroscopic particle of mass 100 g and moving at a velocity of 100 cm s^-1 will have a wavelength of

• 6.6 × 10^-29 cm

• 6.6 × 10^-30 cm

• 6.6 × 10^-31 cm

• 6.6 × 10^-32 cm

For one mole of an ideal gas,the slope of V vs T curve at constant pressure of 2 atm is X L mol^-1 K^-1.The value of the ideal universal gas constant 'R' in terms of X is

• X L atm mol^-1 K^-1

• $\frac{\mathrm{X}}{2}$L atm mol^-1 K^-1

• 2X L atm mol^-1 K^-1

• 2 X atm L^-1 mol^-1 K^-1

At a certain temperature the time required for the complete diffusion of 200-mL of H₂ gas is 30 min. The time required for the complete diffusion of 50 mL of O₂ gas at the same temperature will be

• 60 min

• 30 min

• 45 min

• 15 min

The correct order of decreasing H-C-H angle in the following molecule is

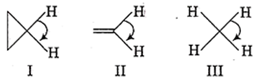
• I > II > III

• II > I > III

• III > II > I

• I > III > II

During the emission of a positron from a nucleus, the mass number of the daughter element remains the same but the atomic number

• is decreased by 1 unit

• is decreased by 2 units·

• is increased by 1 unit

• remains unchanged

β- emission is always accompained by

• formation of antineutrino and α-particle

• emission of α-particle and γ-ray

• formation of antineutrino and γ-ray

• formation of antineutrino and positron

Four gases P, Q, R and S have almost same values of 'b' but their 'a' values (a, b are van der Waals' constants) are in the order Q < R < S < P. At a particular temperature, among the four gases, the most easily liquefiable one is

• P

• Q

• R

• S

The compound that will have a permanent dipole moment among the following is

• I

• II

• III

• IV

The correct order of decreasing length of the bond as indicated by the arrow in the following structures is

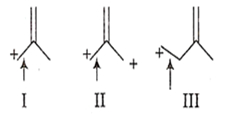
• I > II > III

• II > I > III

• III > II > I

• I > III > II