 Multiple Choice Questions
Multiple Choice QuestionsThe density of a gas A is thrice that of a gas B at the same temperature. The molecular weight of gas B is twice that of A. What will be the ratio of the pressures acting on B and A?
For the reaction, H2 + I2 2HI, K = 47.6. If the initial number of moles of each reactant and product is 1 mole then at equilibrium
[I2] = [H2] , [I2] > [HI]
[I2] = [H2] , [I2] < [HI]
[I2] < [H2] , [I2] = [HI]
[I2] > [H2] , [I2] = [HI]
The AsF5 molecule is trigonal bipyramidal. The hybrid orbitals used by the As atoms for bonding are
dx2-y2, dz2, s, px, py
dxy, s, px, py, pz
dx2-y2, s, px, py
s, px, py, pz, dz2
Hydride of boron occurs as B2H6 but B2Cl6 does not exist. This is because
p - d back bonding is possible in B2H6 but not in B2Cl6
boron and hydrogen have almost equal values of electronegativity
boron and chlorine have almost equal atomic sizes
small hydrogen atoms can easily fit in between boron atoms but large chlorine atoms do not.
Calculate the overall complex dissociation equilibrium constant for the [Cu(NH3)4]2+ ions, given that stability constant () for this complex is 2.1 1013.
8.27 10-13
4.76 10-14
2.39 10-7
1.83 1014
The temperature dependence of a reaction is represented by the Arrhenius equation:
ln k = -
Which among the following is wrong conclusion about the given plot?
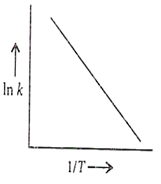
Intercept of the line= ln A
Slope = -
Reaction with high activation energy is more temperature sensitive than that of low activation energy (Ea).
Slope = -
Which of the following oxoacids of phosphorus is a reducing agent and a monobasic acid as well?
H4P2O5
HPO3
H3PO3
H3PO2
Ionisation potential of hydrogen atom is 13.6 eV. Hydrogen atom in ground state is excited by monochromatic light of energy 12.1 eV. The spectral lines emitted by hydrogen according to Bohr's theory will be
one
two
three
four
Ka for HCN is 5 x 10-10 at 25°C. For maintaining a constant pH = 9, the volume of 5 M KCN solution required to be added to 10 mL of 2 M HCN solution is
4 mL
2.5 mL
2 mL
6.4 mL