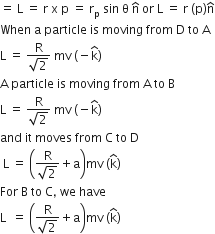A point particle of mass m, moves along the uniformly rough track PQR as shown in the figure. The coefficient of friction, between the particle and the rough track equals µ. The particle is released, from rest, from the point P and it comes to rest at a point R. The energies, lost by the ball, over the parts, PQ and QR, of the track, are equal to each other, and no energy is lost when particle changes direction from PQ to QR. The values of the coefficient of friction µ and the distance x(=QR), are, respectively close to :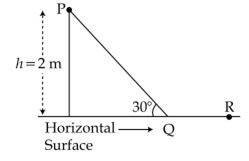
0.2 and 6.5 m
0.2 and 3.5 m
0.29 and 3.5 m
0.29 and 3.5 m
C.
0.29 and 3.5 m
Energy lost over path PQ = μ mg cos θ x 4
Energy lost over path QR = μ mgx
i.e μ mg cos 30° x 4 = μ mgx (∴ θ = 30°)![]()
From Q to R energy loss is half of the total energy loss.
i.e μ mgx = mgh/2
μ = 0.29
The values of the coefficient of friction μ and the distance x (=OR) are 0.29 and 3.5 m
A projectile is given an initial velocity of where is along the ground and
where is along the ground and  is along the vertical. If g = 10 m/s2, the equation of its trajectory is:
is along the vertical. If g = 10 m/s2, the equation of its trajectory is:
y = x-5x2
y = 2x-5x2
4y = 2x- 5x2
4y = 2x- 5x2
B.
y = 2x-5x2
Initial velocity, 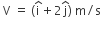
the equation of trajectory of the projectile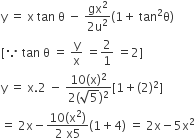
A roller is made by joining together two cones at their vertices O. It is kept on two rails AB and CD which are placed asymmetrically (see figure), with its axis perpendicular to CD and its centre O at the centre of line joining AB and CD (see figure). It is given a light push so that it starts rolling with its centre O moving parallel to CD in the direction shown. As it moves, the roller will tend to: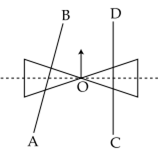
turn left
turn right
go straight
go straight
A.
turn left
As, the wheel rolls forward the radius of the wheel, decreases along AB hence for the same number of rotations it moves less distance along AB, hence it turns left.
Four particles, each of mass M and equidistant from each other, move along a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is
![]()
![]()
![]()
![]()
D.
![]()
Net force acting on any one particle M,
= 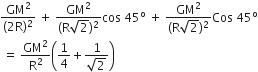
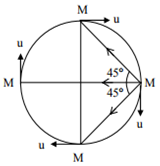
This force will equal to centripetal force
So, ![]()
![]()
A particle of mass m is moving along the side of a square of side ‘a’, with a uniform speed v in the x-y plane as shown in the figure: 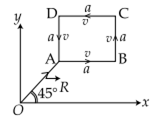
Which of the following statements is false for the angular momentum → L about the origin?




B.

For a particle of mass, m is moving along the side of a square a. Such that
Angular momentum L about the origin