A projectile is moving at 20 ms-1 at its highest point, where it breaks into equal parts due to an internal explosion. One part moves vertically up at 30 ms-1 with respect to the ground. Then the other part will move at
20 ms-1
50 ms-1
30 ms-1
C.
50 ms-1
p1 = mu = m . 20
A body is projected vertically upwards from the surface of a planet of radius R with a velocity equal to half the escape velocity for that planet. The maximum height attained by the body is
R/2
R/3
R/5
R/4
D.
R/4
u = ve/2 , ve = escape velocity of body for that planet
Due to gravity at that planet
The angle between velocity and acceleration of a particle describing uniform circular motion is
180°
90°
45°
60°
B.
90°
When an object follows a circular path at a constant speed, the motion of object is called uniform circular motion. Although the speed does not vary the particle is accelerating because the velocity changes its direction at every point on circular track.
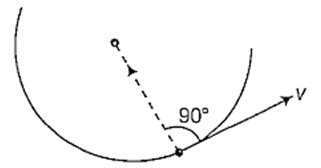
The acceleraton is centripetal, which is perpendicular to motion at every point and acts along the radius and directed towards the centre of the curved circular path.
A body of mass 1 kg begins to move under the action of a time dependent force F = ![]() N, where
N, where ![]() are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
are units vectors along X and Y axis. What power will be developed by the force at the time (t)?
(2t2 + 4t4) W
(2t3 + 3 t4) W
(2t3 + 3t5) W
(2t + 3t3)W
C.
(2t3 + 3t5) W
A body of mass 1 kg begins to move under the action of time dependent force,
F = (2t  +3t2
+3t2  ) N,
) N,
where  are unit vectors along X and Y axis.
are unit vectors along X and Y axis.
F = ma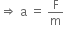
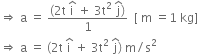
Acceleration, a = 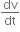

Integrating both sides, we get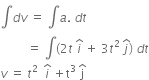
Power developed by the force at the time t will be given as,
P = F.v = (2t  + 3t2
+ 3t2 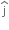 ).(
).(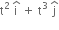 )
)
= (2t. t2 + 3t2.t3)
P = (2t3 + 3t5) W
A very large number of balls are thrown vertically upwards in quick successions in such a way that the next ball is thrown when the previous one is at the maximum height. If the maximum height is 5 m, the number of balls thrown per minute is (take g = 10 m/s2)
80
120
40
60
D.
60
A is the origin from where the ball is thrown.
Let u be the velocity of projection of ball.
∴ v2 = u2 − 2gh (upwards)
At B, v = 0
Ball is projected with 10 m/sec.
Time taken by ball to reach max height
v = u − gt
0 = 10 − 10t
⇒ t = 1 sec
In 1 sec, ball will reach the top and in next 1 sec it will reach the ground again.
∴ 1st ball reaches B in 1 sec.
IInd ball reached B in 1 sec.
When IInd is at B, 1st is at A and so on.
∴ Number of ball projected/sec = 1
Number of ball projected/min = 60
