A particle has initial velocity (2i+3j) and acceleration (0.31i +0.2j). The magnitude of velocity after 10 s will be
 units
units
 units
units
5 units
5 units
B.
 units
units
From the equation of motion, we knows,
v=u+ at
v= (2i+3j)
a=(0.3i +0.2j)
v=(2i+3j) +(0.3i +0.2j) x 10
v=5i+5j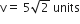
A projectile is fired from the surface of the earth with a velocity of 5 m/s and angle  with the horizontal. Another projectile fired from another planet with a velocity of 3 m/s at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is,
with the horizontal. Another projectile fired from another planet with a velocity of 3 m/s at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth. The value of the acceleration due to gravity on the planet is,
3.5
5.9
16.3
16.3
A.
3.5
If the trajectory is same for both the projectiles, their maximum height will be the same.
That is,
(Hmax)1 = (Hmax)2
i.e., 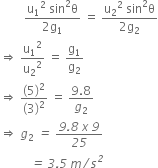
The horizontal range and the maximum height of a projectile are equal. The angle of projection of the projectile is
B.
Given, R = H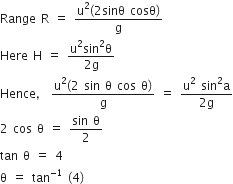
A balloon with mass m is descending down with an acceleration a (where a <g). How much mass should be removed from it so that it starts moving up with an acceleration a?
![]()
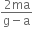
![]()
![]()
A.
![]()
When the balloon is descending down with acceleration a,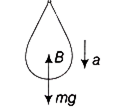
So, mg - B = mx A ... (i)
where B is the buoyant force.
We assume here that while removing same mass, the volume of balloon and hence buoyant force will not change.
Let, us assume the new mass of the balloon is m'.
So, mass removed is (m-m')
Therefore,
B-m'g = m'x a ... (ii)
On solving equations (i) and (ii), we have
mg - B = m x a
B - m'g = m' x a
mg - m'g = ma + m'a
(mg - ma) = m' (g+a) = m (g-a) = m' (g+a)
That is,![]()
That is, mass removed is m-m'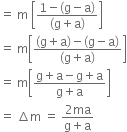
The velocity of a projectile at the initial point A is (2 i + 3 j) m/s. Its velocity (in m/s) at point B is,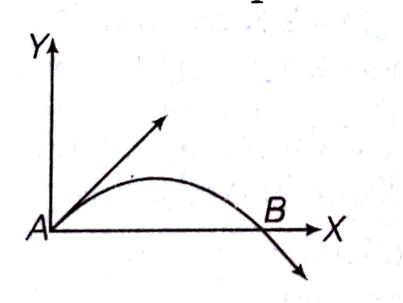
-2 i - 3 j
-2 i + 3 j
2 i - 3 j
2 i - 3 j
C.
2 i - 3 j
From the fig,, the X component remain unchanged, while the Y-component is reverse. Then, the velocity at point B is (2 i - 3 j) m/s.
