Explain how a vector ![]() can be subtracted from vector
can be subtracted from vector ![]()
To subtract vector 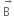 from vector
from vector  first change the vector
first change the vector 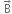 into
into  and then add it to vector
and then add it to vector 
Then, we have

This way, the vectors can be subtracted.
Let ![]() be represented by
be represented by ![]() and
and ![]() the two adjacent sides of parallelogram OPSQ. In the figure
the two adjacent sides of parallelogram OPSQ. In the figure ![]() is the diagonal of parallelogram.
is the diagonal of parallelogram.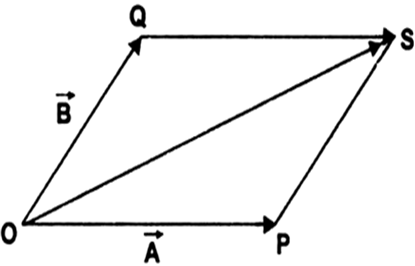
Since ![]() is equal and parallel to
is equal and parallel to ![]()
∴ ![]()
Also ![]() is equal and parallel to
is equal and parallel to ![]()
∴ ![]()
Now applying triangle law of vector addition to ![]() we get
we get
![]() ...(1)
...(1)
Similarly applying triangle law of vector addition to ![]() we get
we get
![]() ...(2)
...(2)
From (1) and (2),
![]()
Hence the vector addition follows commutative law.
![]()

Two vectors of magnitude A and B are acting at angle ![]() . Find the manitude of the difference of two vectors.
. Find the manitude of the difference of two vectors.
Let two vectors  of magnitude A and B be acting at angle
of magnitude A and B be acting at angle ![]()
We will find the magnitude of 
The vector  can be written as
can be written as 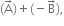 .
.
Thus,  is equal to resultant of
is equal to resultant of 
As the angle between  is
is ![]() , therefore angle between
, therefore angle between  is
is 
Thus,



