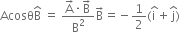A particle moves in XY plane, such that its position at any instant is
![]() and
and ![]()
Find the angle between velocity vector and acceleration vector at any instant.
The position of the particle at any instant is,
![]()
Therefore the velocity of particle at any instant is,



Acceleration of particle at any instant is,



Now, 

Since dot product of acceleration vector and velocity vector is zero, therefore the acceleration vector and velocity vector is 
Find the component of vector ![]() in the direction of
in the direction of ![]()
We know 
∴ ![]()
Now component of ![]() in the direction of
in the direction of ![]() is,
is,
![]()
![]()
Here, ![]()
and ![]()
Thus, ![]()
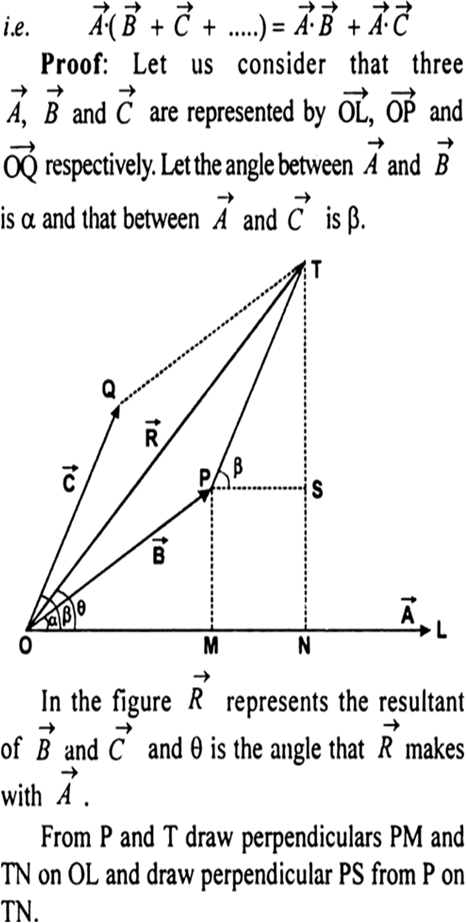
and 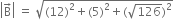
![]()
∴ ![]()
![]()
Find the component of vector ![]() in direction of
in direction of ![]()
Dot product of two vectors is given by,
![]()
∴ ![]()
New component of ![]() in the direction of
in the direction of ![]()
![]()
![]()
Given,
![]() and
and ![]()
Thus,
![]()
Magnitude of B, 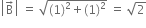
So, components of vector in the direction of 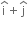
∴