Total pressure P1 = PA + PB + Pc (pressure units)
pA, pB and pc are the partial pressures of A, B and C respectively. When x is the amount of A converted into products, when pi is the initial pressure at time t = 0
where
Pseudo first order reaction: Although in most reactions, order and molecularity are same, there are certain reactions whose order and molecularity differ. For example, hydrolysis of
sugarcane,
Molecularity of this reaction is 2 but its order 1 because its rate depends only on the concentration of surcrose. The concentration of water remains is very high and does not change during the reaction (i.e., concentration of water remains practically constant throughout the reaction). Such reactions are known as pseudo-unimolecular or pseudo first order reactions. Other examples, of pseudo-unimolecular reaction is the acidic hydrolysis of esters where water
remains in excess.
Although it is termolecular (molecularity = 3) reaction, its order is one as concentration of H+ and H2O+ remains constant during reaction. Hydrolysis of organic chlorides is also an example of first order reaction small water (one of the reactants) is again in large excess and its concentration remains constant throughout the reactions.
Thus when one of the reactants is present in large excess, the second order reaction conforms to the first order and is known as a pseudo-unimolecular reaction.
Reaction between acetic anhydride and excess of ethanol to form ester and conversion of N-Chloroacetanilide to p-chloroacetanilide are also examples of pseudo-unimolecular reactions.
The decomposition of H2O2 in basic solution is first order in H2O2.
2H2O2(aq) → 2H2O2 (l) x O2(g)
the rate constant is 1.6 x 10–5 s–1 at 25°C and initial concentration of H2O2 is 0.20 M.
(a) What is the concentration of H2O2 after 2 hrs.
(b) How long will it take for H2O2 concentration to drop to 0.08 M.
(c) How long will it take for 90% of H2O2 to decompose?
(a) ![]()
or ![]()
or ![]()
(b)
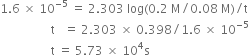
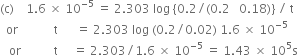
Table 4.2. Integrated rate laws for the reactions of simpler order.
|
t (in mitt) |
0 |
135 |
339 |
683 |
1680 |
|
C (mol L–1) |
2.08 |
1.91 |
1.68 |
1.35 |
0.57 |
Find the order of reaction and calculate its rate constant.
Rate of reaction =
Also, Because
Dependence of rate on concentration of reactants: The rate of a chemical reaction at a given temperature may depend on the concentration of one or more reactants and sometimes on products. The representation of rate of a reaction in the terms of the concentration of the reactants is given by rate law. The rate for a given reaction is established by experimental study of the rate of reaction over a wide range of concentration of the reactants and products. Rate law expression differs for the same reaction under different experimental conditions. Rate constants and order of reaction:
(i) Rate constant or specific reaction rate: It is the rate of reaction when the concentration of each reactant is 1 mol/L. For a given reaction it is constant at a particular temperature and is independent of the concentration of reactants. The units of the rate constant of a reaction depends on the order of the reaction. For an nth order of reaction,
For zero order of reaction, units of k is mol L–1 time–1, for first order reaction, unit of k is time–1, for second order reaction, unit of k is L mol–1 time–1.
In terms of gaseous reactions, concentration is expressed terms of pressure having units of atmosphere. Let us consider the general reaction: aA + bB → Products
where A and B are the reactants and a and b are the stoichiometric coefficients in the balanced chemical equations.
The rate law is written as,
Rate = Δ[A] / Δ t = k[A]α [B]β
where k is called the rate constant. Rate constant (k) is the constant of proportionality within the empirical rate law linking the rate of reaction and concentration of reactants involved in the reaction. The rate law can be written in the form
Rate ∝ [A]α[B]β
The exponents ‘α’ and ‘β’ in the rate law indicate how sensitive the rate is to change in [A] and [B] and they are usually unrelated to the coefficients a and b in the balanced equation. In general, exponents are positive. But for complex reactions it can be negative, zero or even fractions. If exponent is one, it means rate depends linearly on the concentration of the reactant. If concentration of A is doubled, rate is also doubled. This means a = 1. If α = 2 and [A] is also doubled, rate increases by the factor of 4(z2). When exponent is zero {[A]0 = 1}, rate is independent of concentration.
| t/sec | 1242 sec | 2745 sec | 4546 sec |
| At Conc. | -27.80ml | -29.70ml | -31.81ml |
Here [ A]0 is proportional to the alkali consumed between t = &&& and t = 339 sec, i.e., [A]0 = (39.81 mL – 26.34 mL) = 13.47 mL [A]t is proportional to the alkali consumed at &&& minus the alkali consmed at the specified time. Thus,
[A], at 1242 sec = 39.81 mL – 27.80 mL = 12.01 mL
[A], at 2745 sec = 39.81 mL – 29.70 mL = 10.11 mL
[A], at 4546 sec = 39.81 mL – 31.81 mL = 8.00 mL
Substituting the values of t, [A]0 and [A]t in the first-order rate equation
we get the following values of k
(i)
(ii)
(iii)
Since the three values of k derived from first-order reaction are close to being identical, hydrolysis of methyl acetate is a first order reaction.
